Enunciado
Cálculo - Cálculo Volume 2 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 11.12 - Ex. 16
- Aproxime por um polinômio de Taylor com grau em .
- Use a desigualdade de Taylor para estimar a precisão da aproximação quando estiver no intervalo dado.
- Verifique seu resultado na parte b) plotando
Passo 1
E ai, galera, beleza?
Essa questão pede pra gente um monte de coisa, né? Então vamos ver com calma...
- Encontrar o polinômio de Taylor de centrada em
- Estimar a precisão da aproximação de que vamos achar em (a), usando a desigualdade de Taylor:
- Vamos plotar o resto , para verificar o que a gente achar em (b).
Pra isso, vamos usar a fórmula do polinômio de Taylor centrado em :
Ela diz que, em um intervalo
Vamos usar o intervalo
Parece muita coisa, mas vamos passo a passo que fica tranquilo!!
Passo 2
(a)
Vamos começar escrevendo o polinômio de Taylor. Como a questão nos disse que e , o nosso polinômio será:
Portanto, temos que determinar as derivadas e aplicar no ponto . Desta forma,
Portanto, o polinômio de Taylor é:
Passo 3
(b)
A desigualdade de Taylor nos diz que
A gente precisa descobrir quem é esse , que é o valor máximo de , vamos então descobrir primeiro quem é :
Como estamos no intervalo , o valor máximo de vai ser , que acontece quando :
Pra saber isso, é só olhar pro círculo trigonométrico, e ver os valores de seno entre e :
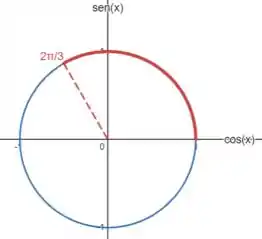
Portanto, podemos tomar como :
Como , o valor de será máximo quando ou , que é quando . Desta forma, temos:
Passo 4
(c)
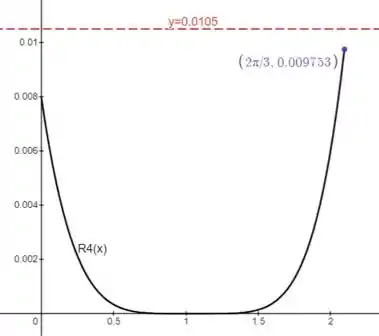
Para compararmos o erro, vamos utilizar softwares para plotar a curva . Portanto, temos:
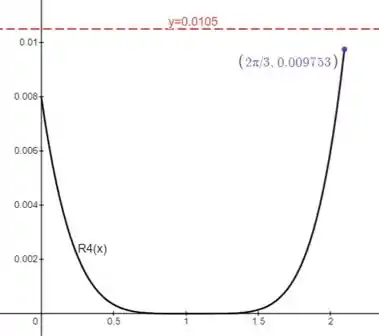
No ponto onde , temos o erro máximo no intervalo, que é menor do que o valor calculado em (b), o que confirma o resultado que
Resposta
- O gráfico está completamente abaixo do valor de , o que confirma o resultado de (b).
