Enunciado
Cálculo - Thomas - Vol 2- Ed: 12º - Capítulo 11.5 - Ex. 20
A área da região que está dentro da curva cardioide e fora do circulo não é
Por que não? Qual é a área? Justifique suas respostas.
Passo 1
Fala gente tudo bem? Exercício tranquilo, como de praxe, devemos saber quem é a nossa figura, para isso vamos utilizar o Geogebra para desenha-la.
Essa é a nossa figura:
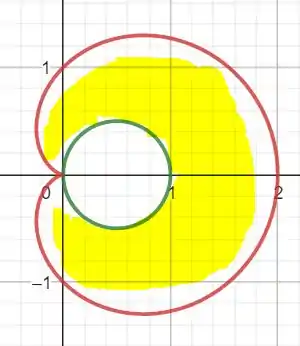
Não podemos utilizar a fórmula enunciada pois a área do círculo não precisa ser integrada, já sabemos ela. Além disse, os limites de integração da cardioide não são de 0 a como vermos a seguir.
Passo 2
Agora, vamos entender qual é a área que devemos calcular.
Como o circulo está dentro da cardioide, devemos primeiro calcular a área da cardioide e depois retirar a área do círculo.
Para o cálculo da cardioide precisamos saber quem são os limites, então:
Lembrando que tem a simetria no eixo y, portanto a área deve ser multiplicada por 2.
Passo 3
Por fim, para saber a área hachurada, basta subtrair a área da cardioide da área do círculo:
Resposta
A área enunciada não pode ser considerada devido pois o círculo está em ambos os eixos de 0 a , portanto, .