Enunciado
Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 3.Exercícios Práticos - Ex. 157
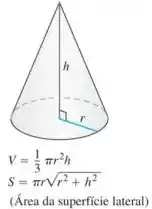
Área de superfície de um cone
Escreva uma fórmula que estime a variação que ocorre na área da superfície lateral de um cone circular reto quando a altura varia de a e o raio não se altera.
Passo 1
A variação na área que desejamos encontrar pode ser definida utilizando o diferencial , já que é a área em questão e a sua derivada representa a taxa de variação. O enunciado também fornece a função e define a altura como a variável e o raio como uma constante.
Passo 2
Aplicando a derivada em função de , tem-se que:
Resposta
Exercícios de Livros Relacionados
Use a diferencial d y para aproximar ∆ y de acordo com as mudanças de x. y = x x 2 + 1 ; d ex = 2p a r ax = 1 , 9 6
Use a diferencial d y para aproximar ∆ y de acordo com as mudanças de x. y = x 8 x + 1 ; d ex = 3p a r ax = 3,05
O lado de um cubo mede aproximadamente 25 cm, com erro possível de ± 1 c m (a) Use diferenciais para estimar o erro no volume calculado.(b) Estime os erros percentuais nos lados e no volume.
O volume de uma esfera é computado a partir do valor medido de seu raio. Estime o máximo erro percentual possível na medida se o erro percentual no volume deve ser mantido em não mais de ± 3 % ( V = 4
Use a diferencial d y para aproximar ∆ y de acordo com as mudanças de x. y = 3 x - 2 ; d ex = 2p a r ax = 2,03