Enunciado
Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 5.6 - Ex. 118a
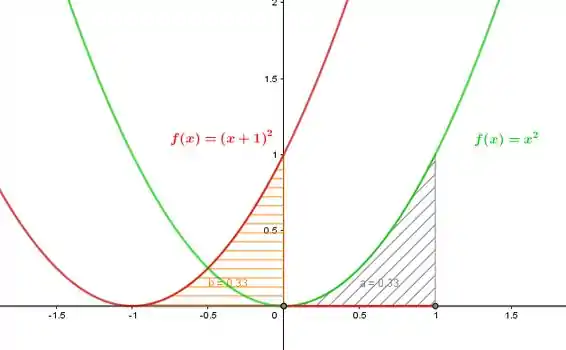
Para cada uma das seguintes funções, faça o gráfico sobre e sobre para se convencer de que a Equação I é razoável.
e
Passo 1
Perceba que o faremos aqui é verificar se do ponto de vista geométrico
Sendo assim vamos verificar se quando encontramos a área de cada uma dessas regiões , elas são de fato iguais.
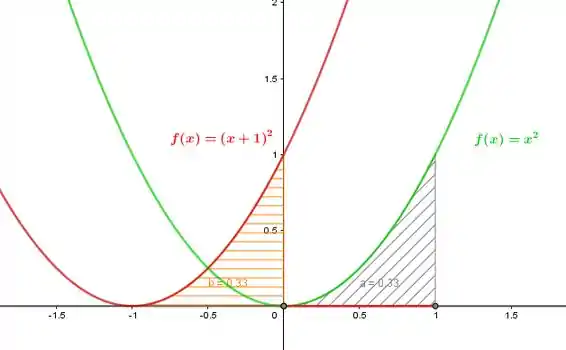
De fato isso ocorre, quando verificamos a área de cada uma das regiões elas são exatamente iguais. Já que corresponde a área da região entre e o eixo corresponde a área região entre e o eixo .
Resposta
Exercícios de Livros Relacionados
Cada uma das seguintes funções resolve um dos problemas de valor inicial dos Exercícios 65-68. Qual função resolve qual problema? Justifique brevemente suas respostas. y = ∫ 1 x 1 t d t - 3 y = ∫ 0 x
Expresse, em termos de integrais, as soluções dos problemas de valor inicial nos exercícios 69 e 70. d y d x = sec x , y 2 = 3
Expresse, em termos de integrais, as soluções dos problemas de valor inicial nos exercícios 69 e 70. d y d x = 1 + x 2 , y 1 = - 2
Demonstre que, se k é uma constante positiva, então a área entre o eixo x e um arco da curva y = sen k x é 2 / k .
Cada uma das seguintes funções resolve um dos problemas de valor inicial dos Exercícios 65-68. Qual função resolve qual problema? Justifique brevemente suas respostas. y = ∫ 1 x 1 t d t - 3 y = ∫ 0 x