Enunciado
Cálculo - Cálculo Volume 1 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 2.9 - Ex. 33
33 (a)Se , encontre
(b) Verifique se sua resposta em (a) foi razoável e comparando os gráficos de e
Passo 1
Olá, meu querido e genial estudante. Vamos para mais uma resolução?
Veja bem, aqui a gente tem a função:
E nos pedem para encontrarmos a derivada de . Para isso, iremos utilizar a fórmula de derivada.
Colocarei aqui a equação para calcular a derivada de :
Após calcularmos a derivada, iremos comparar se o resultado que encontramos faz sentido, faremos isso analisando os gráficos das duas funções.
Passo 2
Vamos então aos cálculos:
Vamos anotar aqui os valores que estão na expressão da derivada!
Realizando o
Para :
Substituindo tudo dentro da derivada, temos:
Realizando o do numerado:
Organizando a divisão de frações:
Simplificando os termos semelhantes:
Botando o em evidência, temos:
Cortando de cima com de baixo, temos:
Passo 3
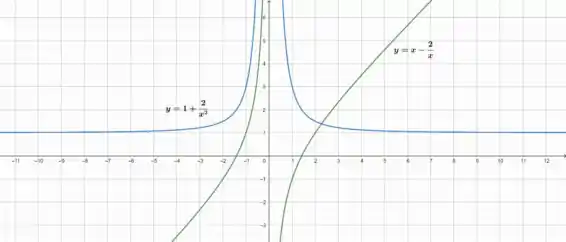
Nesse passo, faremos a análise gráfica de e .
Quando olhamos o gráfico da função , podemos perceber que a função aumenta em ambos os lados do , não considerando o porque não está no domínio da função . Precisamente por aumentar, a função derivada terá valores positivos para todos os , então o gráfico de estará acima do eixo .
Como a linha é a assíntota vertical de , a função derivada se aproximará da constante positiva e essa constante positiva estará em torno de porque a função é simétrica em torno do ponto de inflexão. Portanto, a função terá uma assíntota horizontal e forma simétrica em torno do número . Desenhando a função (parte ) no Geogebra e comparando o gráfico com nossas afirmações, podemos obter a verificação. Portanto,
