Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 1 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 2.8 - Ex. 10

9.(a) Se G ( x ) = x 1 + 2 x , encontre G ' ( a ) e use-o para achar uma equação da reta tangente à curva y = x 1 + 2 x no ponto ( - 1 4 , - 1 2 ) .

(b) Ilustre a parte (a) fazendo o gráfico da curva e a reta tangente na mesma tela.

Passo 1

Olá, meu estudante preferido. Pronto para mais uma resolução?

É bom que sim, pois aqui a gente vai ter que encontrar a derivada da função:

G x = x 1 + 2 x

No ponto genérico x = a . Para isso, a gente vai utilizar a fórmula de derivada:

  G ' ( a ) = lim h → 0 ⁡   G ( a + h ) - G ( a ) h

Já para a equação da reta tangente no ponto - 1 4 , - 1 2 utilizaremos a derivada que encontramos e os pontos dados da seguinte forma:

y - y 0 = G ' - 1 4 x - x 0

Onde ( y 0 , x 0 ) é o ponto dado no enunciado pelo qual a nossa reta tangente deve passar.

O gráfico nós iremos fazer utilizando o GeoGebra, ele irá nos ajudar a saber se visemos um bom trabalho.

Passo 2

Letra a)

Agora que já colocamos as fórmulas no passo anterior, temos que fazer os cálculos dessa situação, vamos com calma para não errar:

Inicialmente, vou anotar algumas coisas que iremos precisar:

G x = x 1 + 2 x

G ( a + h ) = a + h 1 + 2 ( a + h ) = a + h 1 + 2 a + 2 h

G ( a ) = a 1 + 2 a

Colocando tudo na expressão do limite, vamos ter:

G ' a = lim h → 0 ⁡ a + h 1 + 2 a + 2 h - a 1 + 2 a h

Fazendo o m m c do numerador:

G ' a = lim h → 0 ⁡ a + h 1 + 2 a - a ( 1 + 2 a + 2 h ) ( 1 + 2 a + 2 h ) ( 1 + 2 a ) h

Organizando a fração:

G ' a = l i m h → 0 ( a + h ) ( 1 + 2 a ) - a ( 1 + 2 a + 2 h ) h 1 + 2 a + 2 h 1 + 2 a

Realizando os produtos:

G ' a = lim h → 0 ⁡ a + h + 2 a 2 + 2 a h - a - 2 a 2 - 2 a h h 1 + 2 a + 2 h 1 + 2 a

Simplificando os termos semelhantes:

G ' a = l i m h → 0 h h 1 + 2 a + 2 h 1 + 2 a

Vamos simplificar o h da parte de cima com o h da parte de baixo:

G ' a = l i m h → 0 1 1 + 2 a + 2 h 1 + 2 a

G ' a = 1 ( 1 + 2 a ) 2

Passo 3

Agora com G ' ( a ) calculado iremos substituir a = - 1 4 para acharemos a inclinação da tangente nesse ponto e podermos encontrar a nossa reta tangente:

G ' - 1 4 = 1 1 + 2 - 1 4 2

G ' - 1 4 = 1 ( 1 - 1 2 ) 2 = 1 1 4 = 4

Voltando para resolvermos o problema da equação da reta tangente, vai ser mais uma substituição de variáveis. Presta atenção no serviçooo!

y - y 0 = G ' ( - 1 4 ) ( x - x 0 )

Lembrando do ponto que queremos ( - 1 4 , - 1 2 ) :

y - ( - 1 2 ) = 4 ( x - ( - 1 4 ) )

y + 1 2 = 4 x + 1

y = 4 x + 1 2

Passo 4

Letra b)

Aqui iremos então montar o gráfico e ver se estamos realmente certos. Com ajuda do GeoGebra montei os dois gráficos:

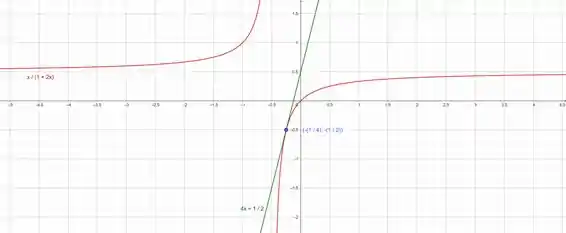
Então terminamos aqui, até uma próxima.

Resposta

(a)

G ' ( a ) = 1 ( 1 + 2 a ) 2

y = 4 x + 1 2

(b)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

32. Ache a taxa de variação instantânea da inclinação da reta tangente ao gráfico y = 2 x 3 - 6 x 2 - x + 1 no ponto ( 3 , - 2 ) .
20 . A c h e f^((5)) (x) s e f (x) = cos (2 x) - s e n ( 2 x )
31. Ache a inclinação da reta tangente em cada ponto do gráfico de y = x 4 + x 3 - 3 x 2 , onde a taxa de variação da inclinação é zero.
37. Ache uma equação da reta tangente à curva y = x 3 - 4 no ponto (2,4).
40. Ache uma equação da reta tangente à curva y = 8 x 2 + 4 no ponto (2,1).