Enunciado
Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 4.1 - Ex. 11
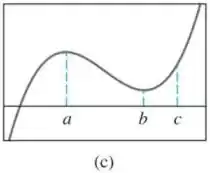
Associe a tabela com um gráfico.
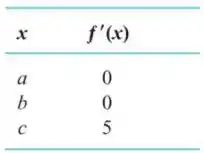
Passo 1
Como a tabela apresenta os valores da primeira derivada da função em questão, podemos fazer uma análise em cima das características definidas pela primeira derivada de uma função (ponto crítico, inclinação).
Passo 2
Como o gráfico mostra que a função possui dois pontos críticos nos pontos e e tem inclinação positiva no ponto , podemos concluir que o gráfico respectivo a essa tabela é o gráfico .
Resposta
Exercícios de Livros Relacionados
7-16. Encontre os valores máximo e mínimo absolutos de f nos intervalos fechados dados e indique onde ocorrem esses valores.16. f x = 6 - 4 x ; - 3 ,3
4. Em cada parte, esboce o gráfico de uma função contínua f com as propriedades indicadas no intervalo - ∞ ,+ ∞ .a) f não tem extremos relativos nem absolutos.b) f tem um mínimo absoluto em x = 0 , ma
Seja: f x = 1 1 - x ,0 ≤ x1 0 ,x = 1 Explique por que f tem um valor mínimo, mas não tem um valor máximo no intervalo fechado 0 ,1 .
17-20. Determine se a afirmação dada é verdadeira ou falsa. Explique sua resposta.20. Se uma função f for contínua em a ,b e f não tiver valores extremos relativos em a ,b , então o valor máximo absol
7-16. Encontre os valores máximo e mínimo absolutos de f nos intervalos fechados dados e indique onde ocorrem esses valores.14. f x = s e nx - cos x ; 0 ,π