Enunciado
Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 4.1 - Ex. 13
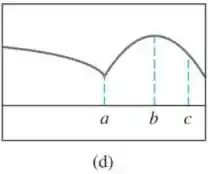
Associe a tabela com um gráfico.
Passo 1
Como a tabela apresenta os valores da primeira derivada da função em questão, podemos fazer uma análise em cima das características definidas pela primeira derivada de uma função (ponto crítico, inclinação).
Passo 2
A informação de que a primeira derivada da função em não existe diz que não há uma reta tangente à curva da função nesse ponto. Além disso, a tabela mostra que o ponto é um ponto crítico e que em a reta tangente à curva possui inclinação negativa.
Logo, conclui-se que o gráfico referente a essa tabela é o gráfico .
Resposta
Exercícios de Livros Relacionados
Mostre que dentre todos os retângulos com área A , o quadrado tem o perímetro mínimo.
Use o Método de Newton para aproximar o mínimo absoluto de f x = 1 4 x 4 + x 2 - 5 x .
Use o Método de Newton para aproximar, com duas casas decimais, as coordenadas x dos pontos de inflexão da função: f x = e - x 1 + x 2
Use o Método de Newton para aproximar o máximo absoluto de f x = 1 - 2 x a r c t gx .
Use o Método de Newton para aproximar o máximo absoluto de f x = xs e nx no intervalo 0 , π .