Enunciado
Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 4.4 - Ex. 20
17-20. Determine se a afirmação dada é verdadeira ou falsa. Explique sua resposta.
20. Se uma função for contínua em e não tiver valores extremos relativos em , então o valor máximo absoluto de existirá e ocorrerá ou em ou em .
Passo 1
Então pessoal, assim como visto na seção 4 do Anton, o Teorema do Valor extremo nos diz que se uma função for contínua em um intervalo finito , então tem um máximo e um mínimo absolutos em . Em outras palavras, o Teorema garante a existência de máximos e mínimos absolutos em um intervalo fechado!
Ok, o enunciado nos diz que não tem extremos relativos dentro do intervalo, então pelo teorema supracitado existirá extremos absolutos em ou em !
Passo 2
Um exemplo disso foi dado pelo próprio Anton na seção em questão, se liga:
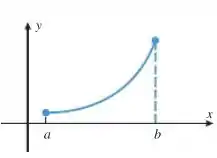
Note que esse é exatamente nosso caso! A função não possui extremos relativos, então obrigatoriamente apresenta extremos absolutos em ou em ! Sendo assim, podemos, com toda certeza, dizer que a afirmação é verdadeira!
Resposta
A afirmação é verdadeira.