Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Thomas - Vol 2- Ed: 12º - Capítulo 14.4 - Ex. 39

Assuma que w = f (s^3 + t^2) e f^' (x) = e^x . Encontre (del w)/(del t) e (del w)/(del s) .

Passo 1

Oi pessoal, primeiramente, pelo enunciado conseguimos identificar que:

x = s^3 + t^2

Pelo nosso diagrama de árvore, temos:

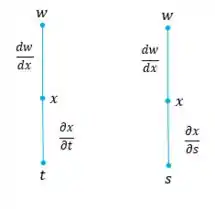
E pela Regra da cadeia:

Sabendo disso, iremos calcular as derivadas del x // del t e del x // del s :

(del x)/(del t) = 2 t

(del x)/(del s) = 3 s^2

Passo 2

E sabemos que:

(d w)/(d x) = f^' (x) = e^(s^3 + t^2)

Substituindo nas equações, encontramos nossas derivadas:

(del w)/(del t) = 2 t e^(s^3 + t^2)

(del w)/(del s) = 3 s^2 e^(s^3 + t^2)

Tchau galerinha, até mais!

Resposta

(del w)/(del t) = 2 t e^(s^3 + t^2) , (del w)/(del s) = 3 s^2 e^(s^3 + t^2) .

Exercícios de Livros Relacionados

17-20. Utilize um diagrama em árvore para escrever a Regra da Cadeia para o caso dado. Suponha que todas as funções sejam diferenciáveis.20. R ( t ,u ) , no qualt = t ( w ,x ,y ,z ) , u = u ( w ,x ,y
Se z = 1 x f x - y + g x + y , mostre que: ∂ ∂ x x ² ∂ z ∂ x = x ² ∂ 2 z ∂ y 2 ² ²
Se z = 1 y f a x + y + g a x - y , mostre que: ∂ 2 z ∂ x 2 = a 2 y 2 ⋅ ∂ ∂ y y 2 ⋅ ∂ z ∂ y
Verificar a regra da cadeia (d f)/(d t) = (del f)/(del x) . (d x)/(d t) + (del f)/(del y) . (d y)/(d t) Para a função f (x , y) = x e^((2 x y^2)) x = 2 t y = 3 t - 1
Determinar (d z)/(d t) , usando a regra da cadeia z = x y , x = 2 t^2 + 1 , y = s e n t