Oi pessoal, vamos lá fazer este exercício juntos!

Como estamos diante da avaliação , vamos seguir os três passos a seguir:

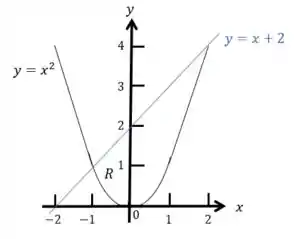
1. Vamos fazer um esboço da região de integração e identificar as curvas limitantes:



Passo 2

2. Para as retas verticais (item a.) vamos imaginar uma reta vertical , que corta na direção de valores de crescentes. Vamos marcar os valores de onde entra e sai de . E iremos escolher os limites de integração de que incluam todas as restas verticais através de :



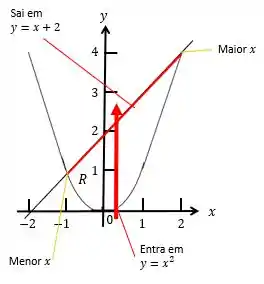
Sendo assim, utilizando as seções transversais verticais, a região de integração de :

Já para a região de , podemos observar que o menor e o maior valor de é quando as curvas se cruzam, ou seja

Resolvendo essa equação de 2° grau:

Logo:

Passo 3

3. Para utilizarmos seções transversais horizontais (item b.) vamos utilizar retas horizontais em vez de verticais:

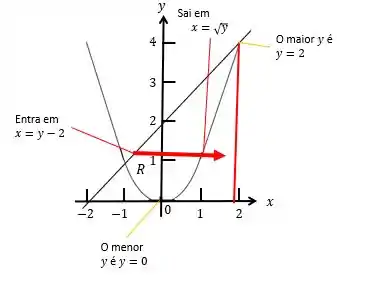
E agora, utilizando as seções transversais horizontais, a região de integração de :

E a região de :

Até mais galerinha!!