Exercícios de Regra da Cadeia – 1 Parâmetro - Lista de Exercícios Resolvida

Suponha que é uma função de classe e

Sabe-se que a curva de equação

Está contida no gráfico da função . Calcule , onde é o valor de no ponto

A temperatura num ponto é , medida em graus Celsius. Um inseto rasteja de modo que sua posição depois de t segundos seja dada por , onde e são medidas em centímetros. A função temperatura satisfaz . Quão rápido a temperatura aumenta no caminho do inseto depois de 3 segundos?

Seja uma função diferenciável e suponha que ela representa a temperatura em graus Celsius em cada ponto de uma sala (as dimensões , e são medidas em metros). Suponha ainda que possui as seguintes propriedades:

Uma mosca está voando por esta sala.

Se a posição em cada instante (dado em segundos) for representada pelo caminho

Determine a taxa de variação da temperatura em relação ao tempo neste caminho, no instante segundos.

Sejam uma função diferenciável no ponto e . Sabendo que

podemos afirmar que vale:

(a) .

(b)

(c)

(d)

(e) nada pode se afirmar

Seja

Suponha

1. Expresse em termos das derivadas parciais de
2. Calcule

Uma montanha tem a superfície descrita por

Um esquiador está no ponto .

Se o esquiador descer a montanha e sua posição em cada instante é dada por

Onde

Determine a componente vertical da velocidade do esquiador, isto é, , quando ele passar pelo ponto .

Seja uma função diferenciável no ponto tal que . Seja . Sabendo que

quanto vale ?

5. Nenhuma das outras alternativas

Seja

a) Calcule as derivadas parciais e .

b) A função é diferenciável em ? Justifique sua resposta.

c) Se , , e definirmos , determine

no ponto .

Seja , onde é diferenciável no plano e são deriváveis num intervalo

(b) Derive para os casos:

onde e .

Seja

c) Considere a curva espacial . Calcule a derivada da função , quando , ou seja, sabendo-se que:

Sendo uma função diferenciável, qual igualdade se verifica para a função ?

Seja

Encontre .

Seja uma função cujo gradiente é dado por . Considere a curva parametrizada por

E a função definida por . Calcule .

Considere a função dada por , em que é uma função diferenciável de uma variável real.

1. Mostre que .

Seja uma função diferenciável. Suponha que exista tal que para todo e . Então, para todo , vale

Seja uma função diferenciável em tal que

Para todo .

Assinale a alternativa da direção e sentido de maior variação da função no ponto :

Seja uma função diferenciável em tal que

Para todo .

Assinale a alternativa da direção e sentido de maior variação da função no ponto :

Seja uma função diferenciável em tal que

Para todo .

Assinale a alternativa da direção e sentido de maior variação da função no ponto :

Considere uma função de três variáveis que tem derivadas parciais contínuas , , em algum intervalo e e são funções de outra variável .

Então .

Diz-se que é a derivada total de em relação a e representa a taxa de variação de à medida que varia.

Supondo onde , , , calcule sendo .

A intensidade de um campo elétrico no plano é dada por uma função diferenciável . Uma partícula de prova passeia ao longo da curva . Sabendo que e , a taxa de variação da intensidade do campo que a partícula experimenta no instante de seu movimento é de:

a) .

b) .

c) .

d) .

e) .

1) Considere a relação definida pela equação .

c. Se , onde , e , calcule ?

Seja uma função diferenciável em tal que

Para todo .

Assinale a alternativa da direção e sentido de maior variação da função no ponto :

Seja , onde F, u e v são diferenciáveis, e

Encontre e

(Capítulo 14.5 – Exercício 37) A velocidade da propagação do som através do oceano com salinidade de 35 partes por milhar foi modelada pela equação

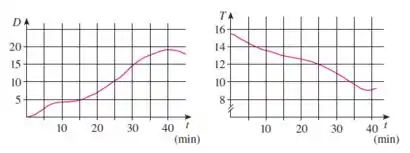
onde C é a velocidade do som (em metros por segundo), T é a temperatura (em graus Celsius) e D é a profundidade abaixo do nível do mar (em metros). Um mergulhador começa um mergulho tranquilo nas águas oceânicas, e a profundidade do mergulho e a temperatura da água ao redor são registradas nos gráficos a seguir. Estime a taxa de variação (em relação ao tempo) da velocidade do som através do oceano experimentada pelo mergulhador 20 minutos depois do início do mergulho. Quais são as unidades?

(Capítulo 14.5 – Exercício 39) O comprimento L, a largura w e a altura h de uma caixa variam com o tempo. Em um determinado momento, as dimensões são e , L e w estão aumentando em uma taxa de 2 m/s enquanto h está decrescendo em uma taxa de 3 m/s. Nesse instante, encontre as taxas em que as seguintes quantidades estão

variando.

(a) O volume

(b) A área da superfície

(c) O comprimento da diagonal

(Capítulo 14.5 – Exercício 40) A voltagem V em um circuito elétrico simples decresce lentamente à medida que a pilha se descarrega. A resistência R aumenta lentamente com o aumento de calor do resistor. Use a Lei de Ohm, , para achar como a corrente I está variando no momento em que , , e

(Capítulo 14.5 – Exercício 45) Suponha que todas as funções dadas são diferenciáveis.

Se , onde e , (a) determine e e (b) mostre que

Seja uma função diferenciável que satisfaz

1. A imagem da curva está contida no gráfico de .
2. , .

Considere, ainda, o ponto .

a) Determine e dê uma equação para a reta tangente à curva em .

b) Calcule e dê a equação do plano tangente ao gráfico de em .

c) A superfície intercepta o gráfico de em uma curva que contém . Determine uma equação para a reta tangente à curva no ponto .

Sejam uma função diferenciável no ponto e . Sabendo que

podemos afirmar que vale:

(a) .

(b)

(c)

(d)

(e) nada pode se afirmar

Considere a função

Que mede a temperatura em de um corpo no espaço. Uma partícula percorre a trajetória dada por

Passando pelo ponto no instante com veor velocidade . A taxa de variação da temperatura da partícula, quando ela se encontra sobre o ponto , será:

14

8

6

Mostre que qualquer função da forma

É uma solução da equação da onda

Onde é uma constante.

A intensidade de um campo elétrico no plano é dada por uma função diferenciável . Uma partícula de prova passeia ao longo da curva . Sabendo que e , a taxa de variação da intensidade do campo que a partícula experimenta no instante de seu movimento é de:

a) .

b) 6.

c) .

d) .

e) .

Seja uma função diferenciável. Sabe-se que o gráfico de contém as imagens das curvas e . Nestas condições, o gradiente de em é paralelo ao vetor:

a) .

b) .

c) .

d) .

e) .

A intensidade de um campo elétrico no plano é dada por uma função diferenciável . Uma partícula de prova passeia ao longo da curva . Sabendo que e , a taxa de variação da intensidade do campo que a partícula experimenta no instante de seu movimento é de:

a) .

b) .

c) .

d) .

e) .

Seja uma função diferenciável. Sabe-se que o gráfico de contém as imagens das curvas e . Nestas condições, o gradiente de em é paralelo ao vetor:

a) .

b) .

c) .

d) .

e) .

Use a regra da cadeia para achar onde e

A temperatura (em graus Celsius ) em uma placa de metal é dada por , onde e são medidos em centímetros. Um objeto está no ponto .

Se o objeto percorrer uma curva e sua posição em cada instante (segundos) é dada por , determine sua taxa de variação de temperatura em relação ao tempo quando ele passar pelo ponto .

1.1. Calcule e pela regra da cadeia e confira os resultados por meio de substituição seguida de aplicação das regras de derivação parcial.

b. ; , .

1.1. Calcule e pela regra da cadeia e confira os resultados por meio de substituição seguida de aplicação das regras de derivação parcial.

a. ; , .

Se

E

Calcule

Seja uma função diferenciável. Sabe-se que o gráfico de contém as imagens das curvas e . Nestas condições, o gradiente de em é paralelo ao vetor: