Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 14.5 - Ex. 20

17-20. Utilize um diagrama em árvore para escrever a Regra da Cadeia para o caso dado. Suponha que todas as funções sejam diferenciáveis.

20. R ( t ,   u ) , no qual   t = t ( w ,   x ,   y ,   z ) , u = u ( w ,   x ,   y ,   z ) .

Passo 1

Hello, meu brother. Vamos de mais uma resolução?!

Temos uma função dada por 2 variaveis:

R t , u

E essas variáveis são em função de outras variáveis:

t = t ( w , x ,   y ,   z )

u = u ( w , x ,   y ,   z )

Devemos então utilizar um diagrama em arvore para encontrar as derivadas parciais:

∂ R ∂ w   ; ∂ R ∂ x   ; ∂ R ∂ y   ; ∂ R ∂ z

Que necessitam da regra da cadeia para serem encontradas, já que temos aqui composições de funções.

Passos para construir o diagrama em árvore:

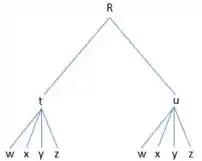
  1. Raiz do diagrama: A função R .
  2. Primeiro nível: As funções t , e u , que são argumentos de R .
  3. Segundo nível: As variáveis w ,   x , y e z , que são argumentos de t e u .

Passo 2

Fazendo o diagrama de árvore para facilitar a visualização das variáveis, teremos:

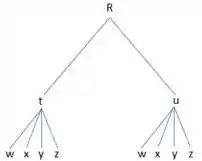
Então para a gente utilizar a arvore a gente faz o seguinte:

Identifique as relações de derivadas parciais:

  • Para cada variável intermediária ( t ,   u ), identifique as derivadas parciais da função principal ( R ) em relação a elas.
  • Para cada variável básica ( w ,   x , y , z ), identifique as derivadas parciais das variáveis intermediárias ( t , u ) em relação a elas.
  • Para cada variável básica ( w ,   x , y , z ), some os produtos das derivadas parciais de cada caminho da raiz até a variável básica.

Para encontrar a derivada de R em relação a w fazemos então:

Caminho 1 : R → t → w

∂ R ∂ t ⋅ ∂ t ∂ w

Caminho 2 : R → u → w

∂ R ∂ u ⋅ ∂ u ∂ w

Somando todos os caminhos, obtemos:

∂ R ∂ w = ∂ R ∂ t ∂ t ∂ w + ∂ R ∂ u ∂ u ∂ w

Realizando o equivalente para os outros caminhos a gente encontra:

∂ R ∂ x = ∂ R ∂ t ∂ t ∂ x + ∂ R ∂ u ∂ u ∂ x

∂ R ∂ y = ∂ R ∂ t ∂ t ∂ y + ∂ R ∂ u ∂ u ∂ y

∂ R ∂ z = ∂ R ∂ t ∂ t ∂ z + ∂ R ∂ u ∂ u ∂ z

E está aí nossas derivadas!

Resposta

∂ R ∂ w = ∂ R ∂ t ∂ t ∂ w + ∂ R ∂ u ∂ u ∂ w

∂ R ∂ x = ∂ R ∂ t ∂ t ∂ x + ∂ R ∂ u ∂ u ∂ x

∂ R ∂ y = ∂ R ∂ t ∂ t ∂ y + ∂ R ∂ u ∂ u ∂ y

∂ R ∂ z = ∂ R ∂ t ∂ t ∂ z + ∂ R ∂ u ∂ u ∂ z

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Nos Exercícios 7 e 8, (a) expresse ∂ z / ∂ ue∂ z / ∂ y como funções de uev utilizando a regra da cadeia e também expressando z diretamente em termos de uey antes de diferenciar. Em seguida, (b) calcul
Nos Exercícios 7 e 8, (a) expresse ∂ z / ∂ ue∂ z / ∂ y como funções de uev utilizando a regra da cadeia e também expressando z diretamente em termos de uey antes de diferenciar. Em seguida, (b) calcul
Nos Exercícios 9 e 10, (a) expresse ∂ w / ∂ ue∂ w / ∂ y como funções de uey utilizando a regra da cadeia e também expressando w diretamente em termos de uey antes de diferenciar. Em seguida, (b) calcu
Encontre dw/dt em t = 0 se w = sen (xy + p), x = et e y = ln (t + 1).
Encontre ∂w/∂r e ∂w/∂s quando r = p e s = 0 se w = sen (2x – y), x = r + sen s, y = rs.