Na ausência de amortecimento, o movimento de um sistema mola-massa satifez o problema de valor inicial
(a) Mostre que a energia cinética dada inicialmente à massa é e que a energia potencial armazenada inicialmente na mola é , de modo que a energia total inicial do sistema é .
(b) Resolva o problema de valor inicial dado
(c) Usando a solução do item (b), determine a energia total no sistema em qualquer instante . Seu resultado deve confirmar o príncipio de conservação de energia para este sistema.
Passo 1
Obs: O enunciado da versão 10 do Boyce apresenta o erro na equação. O termo que acompanha é e não . Isso pode ser percebido pelo próprio enunciado quando o mesmo informa que não há amortecimento.
Primeira coisa que devemos perceber sem nem tentar resolver nosso problema, é que ele se refere a um oscilador armonico infinito.
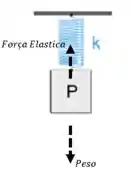
Aqui temos uma ilustração do nosso sistema físico
Passo 2
Sabendo que temos uma massa oscilando com a ajuda de uma mola, vamos olhar para as condições iniciais e entender o que elas nos diz.
Vamos equacionar o problema com base na ilustração do passo 1
Na qual é a constante da mola, o deslocamento que a mola sofre ao se colocar uma massa presa a ela, é a massa e a aceleração da gravidade.
Seja a Energia Potencial dada por definição
Se a mola deslocou uma distância de seu tamanho original ao colocarmos a massa presa a ela, temos que a energia potencial é dada em por
O mesmo discutiremos para a Energia Cinética, que é dada por definição por
Em temos que como é dado pelo condição inicial, assim temos que a Energia Cinética inicial é
Por fim temos que a energia total é dada pela soma de todas as energia presente no sistema. Entretanto só temos duas energia presente em um sistema massa mola, Potêncial e Cinética, Assim
Passo 3
Agora vamos resolver nosso problema de valor inicial. Existe várias maneiras de resolver nosso problema. Um deles é supor uma solução dada por e tentar achar a raízes do nosso problema.
Seguinte esse procedimento, chegamos na nossa solução característica dada por
Na qual definimos que
Desta forma temos que
Que sugere para gente uma solução
Vamos trabalhar com a segunda forma de escrever nossa solução, que parece ser mais fácil. Assim tome as condições iniciais como
Assim já conseguimos determinar que
E nossa solução geral é
Passo 4
Agora vamos fazer o seguinte, seja
Então
Assim, primeira a energia Potencial
e a energia cinética
Assim temos que a energia Total é dada por
Como lembramos , então
E
Além disso temos que
Assim nossa energia total se transforma em
Ou seja, nossa energia total é contante ao longo do tempo.
Resposta
Ei, a resposta está no passo a passo :)