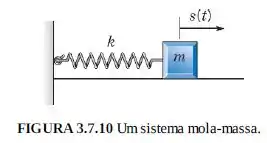
Suponha que uma massa desliza sem atrito em uma superfície horizontal. A massa está presa a uma mola com constante , como ilustrado na Figura , e está sujeita, também,à resistência viscosa do ar com coeficiente . Mostre que o deslocamento da massa a partir de sua posição de equilíbrio satifaz a Como a dedução da equação de movimento deste caso difere da dedução dada no texto?

Pelo enunciado, ainda temos uma mola com constante oscilando, com uma massa presa a ponta e sofrento uma resistência somente do ar , assim temos que

Vamos tomar a Segunda Lei de Newton

Só que, quais são as forças descritas no sistema?

O texto sugere que uma mola com constante , ou seja, toda vez que a massa se descola para uma lado a uma distância em relação ao equilíbri, temos que aparece uma força .

Outra força discutida é a da resitência do ar. Sabemos que a forma de resistência é descrita pela resistência do ar vezes a velocidade que o corpo tem naquele instante, ou seja, .

Ambas as forças trazem o sinal negativo, pois são forças que se opõem ao movimento da massa. Assim pela segunda lei de Newton, temos que a somatória de todas as força em um corpo deve ser então

Assim

A mesma equação da Eq.(21)