Enunciado
Cálculo - Cálculo Volume 1 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 5.5 - Ex. 61
Avalie a integral definida.
Passo 1
Opa, bora calcular essa integral:
Esse é um caso especial. Vamos aplicar o método da substituição para Integrais Definidas para simplificar o cálculo de integrais de funções que possuam propriedades de simetria.
O motivo da gente fazer isso é que os limites de integração são iguais em módulo com sinais diferentes.
Passo 2
Uma função ser par significa que ela possui a mesma forma ao ser refletida em torno do eixo , o que significa .
Uma função ser ímpar significa que ela possui forma oposta ao ser refletida em torno do eixo , o que significa .
Verificamos se a função é ímpar ou par, fazendo:
Resolvendo o, temos:
Temos então que:
Isso significa que a nossa função é ímpar! Pra a gente entender melhor, vamos olhar o gráfico:
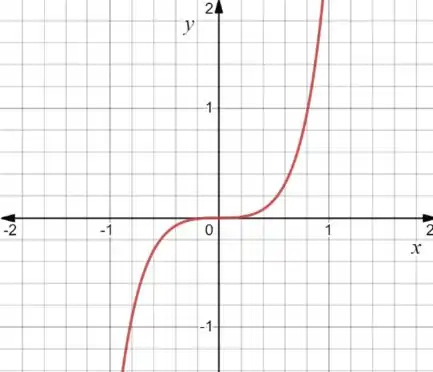
E lembram que a integral de uma função é a área embaixo da curva? E que nas áreas embaixo
do eixo x, a integral é negativa?
Repara que a área sob a curva do eixo positivo é do mesmo tamanho que a do negativo!
Ou seja, uma área “cancela” a outra
Portanto:
Prontinho!