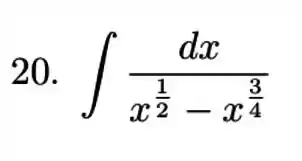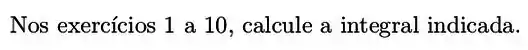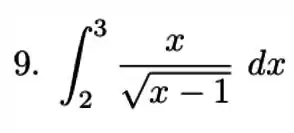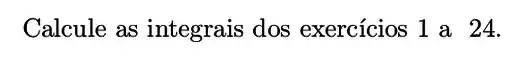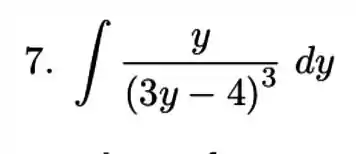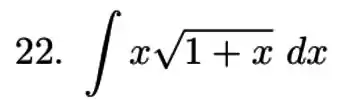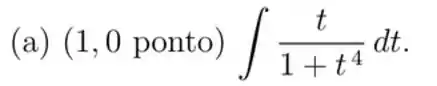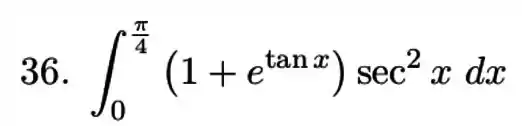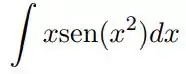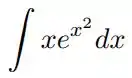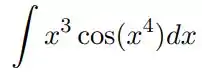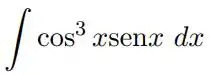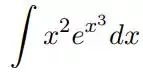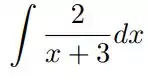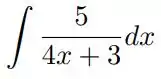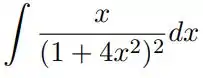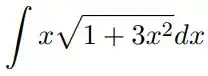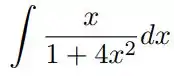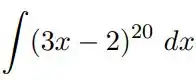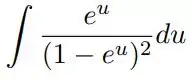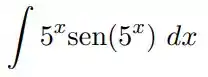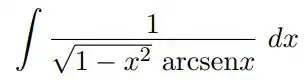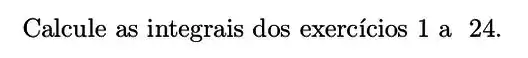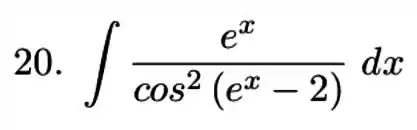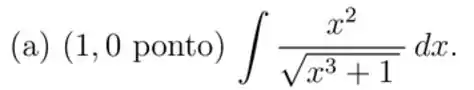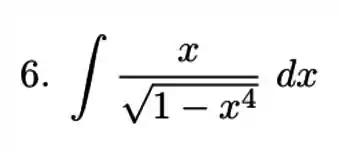Exercícios de Integrais com Substituição Simples - Lista de Exercícios Resolvida
Questão 18
Utilizando a integração por substituição e , calcule cada uma das integrais indefinidas:
Ver solução completaQuestão 29
2. Regra de Substituição
o)
dica: Essa questão é um pouco diferente. Tome Logo,
Você pode pensar agora “Tá, mas o que faço nessa passagem, já que não aparece essa expressão no denominador da integral para trocar por ?” Mas você sabe o que , então
Ou seja . Ache agora uma maneira de expressar o no denominador da integral e finalize a questão.
Ver solução completaQuestão 40
1) Calcule cada uma das seguintes integrais e determine se for convergente ou não conforme corresponda:
a)
Ver solução completaQuestão 55
1.5. Calcule as integrais abaixo usando substituição (inverso da regra da cadeia para derivadas):
(a)
Ver solução completaQuestão 56
1.5. Calcule as integrais abaixo usando substituição (inverso da regra da cadeia para derivadas):
(b)
Ver solução completaQuestão 58
1.8. Calcule
Dica: use o método mágico de multiplicar e dividir o integrando por e depois use substituição.
Ver solução completaQuestão 68
2.7. Calcule
(Dica: a função é ímpar, pense no seu gráfico e na área abaixo dele)
Ver solução completaQuestão 71
4.7. Calcule e explique por que que esta integral pode ser usada para calcular a área do círculo unitário.
Ver solução completaQuestão 88
Nos exercícios de a , resolva a integral indicada. Em alguns casos será preciso aplicar mais de uma técnica de integração.
7)
Ver solução completaQuestão 90
Nos exercícios de a , resolva a integral indicada. Em alguns casos será preciso aplicar mais de uma técnica de integração.
11)
Ver solução completaQuestão 92
Nos exercícios a , resolva a integral indicada. Em alguns casos será preciso aplicar mais de uma técnica de integração.
16)
Ver solução completaQuestão 93
Nos exercícios a , resolva a integral indicada. Em alguns casos será preciso aplicar mais de uma técnica de integração.
19)
Ver solução completaQuestão 94
Nos exercícios a , resolva a integral indicada. Em alguns casos será preciso aplicar mais de uma técnica de integração.
20)
Ver solução completaQuestão 97
Calcule . (*Antes de resolver, procure memes sobre esta integral na internet, existem alguns ótimos.*)
Ver solução completaQuestão 98
Determine a convergência de e, caso seja convergente, determine seu valor.
Ver solução completaQuestão 111
Use uma mudança de variáveis (substituição) para demonstrar as duas afirmações abaixo. Em seguida, faça uma interpretação geométrica de cada uma delas.
- Se é par então
Questão 122
Resolva as integrais seguintes:
c) Inspirada em prova do semestre passado
Ver solução completaQuestão 127
Resolva as integrais seguintes:
f) Integral do Alexandre Pato (SQ1759)
Ver solução completaQuestão 148
Nos exercícios a , resolva a integral indicada. Em alguns casos será preciso aplicar mais de uma técnica de integração.
8)
Ver solução completaQuestão 150
Nos exercícios a , resolva a integral indicada. Em alguns casos será preciso aplicar mais de uma técnica de integração.
18)
Ver solução completaQuestão 153
Considere contínua definida pelo gráfico abaixo e definida por . Mostre que .
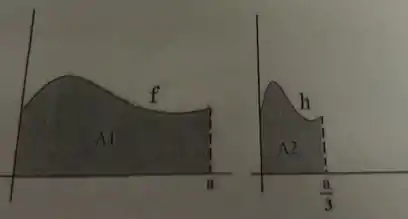
Questão 165
Encontre o volume de uma pirâmide cuja base é o quadrado de lado e cuja altura é .
Ver solução completaQuestão 169
Deseja-se calcular a área sob o gráfico da função para .
a) Explique, por meio de um teorema, por que utilizamos uma primitiva da função para o cálculo da área sob seu gráfico.
b) Utilize a substituição e reescreva a integral apenas em termos da variável .
c) Utilize a substituição e reescreva a integral apenas em termos da variável .
d) Escolha um dos itens acima para determinar a área desejada.
Ver solução completaQuestão 174
Em geral, a regra da substituição de variável não aparece nas tabelas de integrais. Precisamos saber que uma integral em uma determinada variável (por exemplo x) pode ser escrita em uma outra variável (por exemplo u) se fizermos todas as substituições na função a ser integrada e também no termo . Como exemplo, considere .
- Calcule a derivada de
- Escreva em função de e
- Escreva em termos de e
- Escreva em função de
- Escreva em termos de e
- Escreva em termos de e
Questão 177
Em geral, a regra da substituição de variável não aparece nas tabelas de integrais. Precisamos saber que uma integral em uma determinada variável (por exemplo x) pode ser escrita em uma outra variável (por exemplo u) se fizermos todas as substituições na função a ser integrada e também no termo . Como exemplo, considere .
- Use a substituição do enunciado para resolver a integral
Questão 181
Em geral, a regra da substituição de variável não aparece nas tabelas de integrais. Precisamos saber que uma integral em uma determinada variável (por exemplo x) pode ser escrita em uma outra variável (por exemplo u) se fizermos todas as substituições na função a ser integrada e também no termo . Como exemplo, considere .
- Refaça todos os itens iniciando pela expressão obtida no item (d)
Questão 182
Em geral, a regra da substituição de variável não aparece nas tabelas de integrais. Precisamos saber que uma integral em uma determinada variável (por exemplo x) pode ser escrita em uma outra variável (por exemplo u) se fizermos todas as substituições na função a ser integrada e também no termo . Como exemplo, considere .
- Use a substituição do enunciado para resolver a integral
Questão 240
Seja uma função contínua que não se anula para tal que é satisfeito:
- Calcule para esse intervalo, se for necessário usar uma integral, aplique primeiro uma substituição e depois uma integral por frações parciais, outros métodos serão desconsiderados.
- Calcule .
Questão 242
1 Seja uma função contínua no intervalo tal que . Considere
O valor de é
Ver solução completaQuestão 250
- Seja g uma função com derivada contínua no intervalo , tal que e . Calcule a integral .
Ver solução completaQuestão 256
seja a taxa de consumo mundial de petróleo, em que é medido em anos começando em em janeiro de e é medida em barris por ano
b) Se a taxa de consumo é dada por , determine o consumo mundial de petróleo entre o ano de e o ano , para qualquer
Ver solução completaQuestão 272
Seja uma função diferenciável com derivada contínua, tal que e . Calcule .
c)
Ver solução completaQuestão 288
Se necessário, reescreva os integrando de forma adequada para calcular as seguintes integrais, usando a tabela. Em seguida, derive seus resultados para conferir as respostas:
Ver solução completaQuestão 346
Calcule as integrais abaixo usando a Regra de Substituição, quando necessário.
Ver solução completaQuestão 348
Calcule as integrais abaixo usando a Regra de Substituição, quando necessário.
Ver solução completaQuestão 349
Calcule as integrais abaixo usando a Regra de Substituição, quando necessário.
Ver solução completaQuestão 351
Lembrando que duas funções que possuem a mesma derivada em um intervalo diferem por uma constante, determine a função que satisfaz as condições abaixo.
e o gráfico de passa pelo ponto
Ver solução completaQuestão 352
Calcule as integrais abaixo usando a Regra de Substituição, quando necessário.
Ver solução completaQuestão 362
Após identificar a técnica apropriada, determine o valor das integrais abaixo
Ver solução completaQuestão 402
Questão 5
Determine se a integral
É convergente ou divergente. Se for convergente, calcule seu valor.
Ver solução completaQuestão 403
Calcule cada uma das seguintes integrais e determine se for convergente ou não conforme corresponta:
b)
Ver solução completaQuestão 404
Um trem de toneladas parte do repouso e seus motores lhe fornecem uma força de Newtons. Considerando o atrito do ar, é possível mostrar que a velocidade, , do trem satisfaz a equação .
a) Use a substituição e integre com respeito ao tempo.
b) Integre a equação acima e determine em função de uma constante arbitrária de integração.
c) Sabendo que , determine a constante arbitrária do item acima. Em seguida, calcule a velocidade do trem após um longo período de tempo.
Ver solução completaQuestão 429
Calcule cada uma das seguintes integrais e determine se for convergente ou não conforme corresponta:
c)
Ver solução completaQuestão 430
Use uma mudança de variáveis (substituição) para demonstrar as duas afirmações abaixo. Em seguida, faça uma interpretação geométrica de cada uma delas.
b) Se é ímpar então
Ver solução completaQuestão 437
O gráfico da função é dado na figura ao lado. Calcule as integrais a seguir, interpretando-as em termos de áreas:
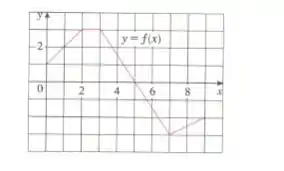
Questão 438
Calcule cada integral definida a seguir, interpretando- a em termos de áreas:
d)
Ver solução completaQuestão 439
Calcule cada integral definida a seguir, interpretando- a em termos de áreas:
a)
Ver solução completaQuestão 440
Calcule cada integral definida a seguir, interpretando- a em termos de áreas:
c)
Ver solução completaQuestão 442
Calcule cada integral definida a seguir, interpretando- a em termos de áreas:
b)
Ver solução completaQuestão 443
Seja , em que é a função cujo gráfico é mostrado na figura. Dentre os valores , decida qual é o maior e qual é o menor.
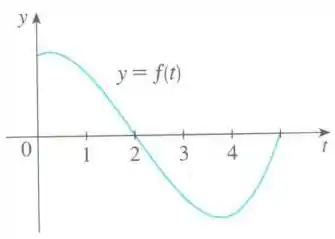
Questão 445
A figura abaixo mostra o gráfico de uma função e destaca três regiões: e , todas com área igual a . Determine as seguintes integrais:
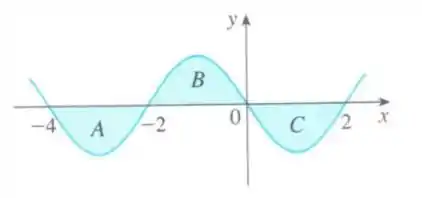
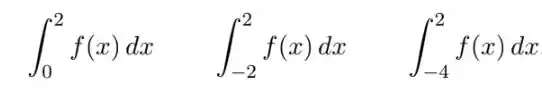
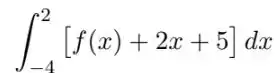
Questão 453
Suponha que a temperatura de um corpo imerso em um meio com temperatura constante e igual a seja tal que graus Celsius. Segundo a Lei do Resfriamento de Newton, a taxa de variação é proporcional à diferença entre as temperaturas e . Supondo que a constante de proporcionalidade seja igual a , segue que
A partir dos dados apresentados, determine a temperatura .
Determine o instante em que .
O que acontece com a temperatura após muito tempo?
Ver solução completaQuestão 455
Uma partícula de massa se move retilineamente sob a ação de uma força que é proporcional à velocidade da partícula e atua em sentido contrário ao deslocamento. Desse modo , com constante. Supondo que resolva os itens a seguir.
De acordo com a Segunda Lei de Newton, temos que , em que é a aceleração da partícula. Usando essa informação e a expressão para dada no enunciado, obtenha a equação que relaciona , , e .
Lembrando que a derivada de é igual a , use o item anterior para obter em termos de , e .
Determine o espaço percorrido pela partícula até o instante , supondo .
Calcule a distância total percorrida pela partícula, dada por .
Ver solução completaQuestão 468
3. Um trem de parte do repouso e seus motores lhe fornecem uma força de . Considerando o atrito do ar, é possível mostrar que a velocidade, , do trem satisfaz a equação.
- Use a substituição e integre com respeito ao tempo.
- Integre a equação acima e determine em função de uma constante arbitrárica de integração
- Sabendo que , determine a constante arbitrária do item acima. Em seguida, calcule a velocidade do trem após um longo período de tempo.
Questão 481
Para a integral abaixo, determine seu valor ou decida sobre sua convergência.
Ver solução completaQuestão 491
Suponha que a receita marginal de uma empresa pela fabricação e venda da baterias seja onde é medido em milhares de reais e milhares de unidades. Quanto dinheiro a companhia deve esperar de uma população de mil baterias? Para isto integre o rendimento marginal de a .
Ver solução completaQuestão 492
Se necessário, reescreva os integrandos de forma adequada para calcular as seguintes integrais, usando a tabela. Em seguida, derive seus resultados para conferir as respostas:
Ver solução completaQuestão 493
Se necessário, reescreva os integrandos de forma adequada para calcular as seguintes integrais, usando a tabela. Em seguida, derive seus resultados para conferir as respostas:
Ver solução completaQuestão 494
Se necessário, reescreva os integrandos de forma adequada para calcular as seguintes integrais, usando a tabela. Em seguida, derive seus resultados para conferir as respostas
Ver solução completaQuestão 495
Questão 1. Calcule cada uma das seguintes integrais e determine se for convergente ou não conforme corresponda:
c)
Ver solução completaQuestão 496
Se necessário, reescreva os integrandos de forma adequada para calcular as seguintes integrais, usando a tabela. Em seguida, derive seus resultados para conferir as respostas
Ver solução completaQuestão 497
2. Mediante o uso de uma tabela, calcule cada uma das seguintes integrais indefinidas.
Ver solução completaQuestão 498
2. Mediante o uso de uma tabela, calcule cada uma das seguintes integrais indefinidas.
Ver solução completaQuestão 500
Utilizando a integração por substituição e , calcule cada uma das integrais indefinidas:
Ver solução completaQuestão 501
Utilizando a integração por substituição e , calcule cada uma das integrais indefinidas:
Ver solução completaQuestão 502
Utilizando a integração por substituição e , calcule cada uma das integrais indefinidas:
Ver solução completaQuestão 503
Utilizando a integração por substituição e , calcule cada uma das integrais indefinidas:
Ver solução completaQuestão 504
Utilizando a integração por substituição e , calcule cada uma das integrais indefinidas:
Ver solução completaQuestão 505
Utilizando a integração por substituição e , calcule cada uma das integrais indefinidas:
Ver solução completaQuestão 506
Utilizando a integração por substituição e , calcule cada uma das integrais indefinidas:
Ver solução completaQuestão 507
Utilizando a integração por substituição e , calcule cada uma das integrais indefinidas:
Ver solução completaQuestão 508
Utilizando a integração por substituição e , calcule cada uma das integrais indefinidas:
Ver solução completaQuestão 537
Utilizando a integração por substituição e , calcule cada uma das integrais indefinidas:
Ver solução completaQuestão 538
Utilizando a integração por substituição e , calcule cada uma das integrais indefinidas:
Ver solução completaQuestão 568
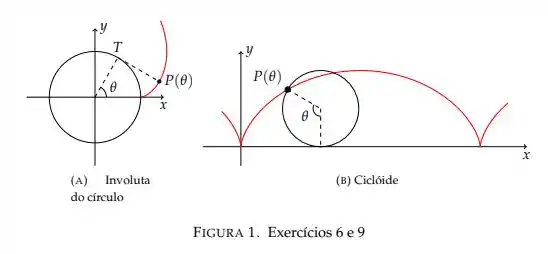
Uma circunferência de raio rola sem escorregar ao longo do eixo . Encontre equações paramétricas para a curva descrita por um ponto da circunferência que se encontra inicialmente na origem. (Esta curva é chamada ciclóide, veja a Figura 1(b))
Questão 584
Regra de Substituição
Final.
Dica: É muito comum que a substituição seja apenas para você conseguir “cancelar” parte do numerador com o denominador. Tente .
Ver solução completa