Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 16.7 - Ex. 30

Avalie a integral de superfície ∬ F ⋅ d S para o campo vetorial F e a superfície S . Em outras palavras, localize o fluxo de F através de S . Para superfícies fechadas, use a orientação (para o exterior) positiva.

F x , y , z = x i + y j + 5 k

S é a região limitada pelo cilindro x 2 + z 2 = 1 e os planos y = 0 e x + y = 2 .

Passo 1

E aê, galera!

Precisamos calcular a integral de superfície dada pelo campo vetorial:

F x , y , z = x i + y j + 5 k

Na superfície S limitada pelo cilindro

x 2 + z 2 = 1

E pelos planos

y = 0

x + y = 2

Galera, veja que temos temos que a superfície S é composta por três: S 1 ,   S 2 e S 3 .

Onde S 1 é o disco circular no plano y = 0 , S 2 é o disco elíptico no plano x + y = 2 e S 3 é a parte curva do cilindro. Por convenção, os vetores normais apontam para fora da superfície. Vamos calcular cada um e depois somar.

Veja o gráfico:

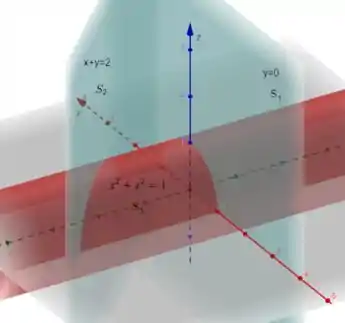
Passo 2

Vamos primeiro começar calculando com o fluxo da superfície em S 1 . Vamos ter essa fórmula aqui:

∬ F ⋅ d S

Sabemos que n   é o vetor normal que mostra a direção do fluxo em:

d S = n   d S

Para a superfície S 1 o vetor normal está apontando para o sentido negativo do eixo y . Logo,

n = - j

Portanto,

d S = - j   d S

Logo, o fluxo por S 1 será dado por:

∬ x i + y j + 5 k ⏟ F - j d S

Como temos um fluxo em y , então:

∬ - y d S

Todos os pontos de S 1 estão contidos no plano y = 0 . Logo,

∬ 0 d S = 0

Passo 3

Galerinha, uma maneira de calcular o fluxo por S 2 é com a fórmula do item anterior:

∬ F ⋅ d S = ∬ F ⋅ n d S

onde n é o vetor unitário normal e

d S = r u × r v d A

O fluxo através da superfície é definido somente se a superfície for orientável. Note que se a superfície é orientável, terão dois vetores normais em todos os pontos. Podemos escrever:

d S = n d A = ± r u × r v r u × r v   r u × r v d A = ± r u × r v d A

Para encontrar o fluxo, nós sempre usamos n que corresponde a orientação positiva.

S 2 é a parte do plano x + y = 2 que está dentro do cilindro x 2 + z 2 = 1 . A representação paramétrica de S 2 é:

( v sen ⁡ u ,   - v sen ⁡ u ,   v cos ⁡ u )

onde v ∈ ( 0,1 ) e u ∈ ( 0,2 π ) . Assim,

r u = v cos ⁡ u i - v cos ⁡ u j - v sen ⁡ u k

r v = sen ⁡ u i - sin ⁡ u j + cos ⁡ u k

Precisamos agora encontrar o valor de r u × r v !

r u × r v = i j k v cos ⁡ u - v cos ⁡ u - v sen ⁡ u sen ⁡ u - sen ⁡ u cos ⁡ u

r u × r v = - v i - v j + 0 k

Como v > 0 , r u × r v está apontando para dentro. Assim,

d S = - r u × r v d a = v i + j d A

Passo 4

Resolvendo a integral, temos:

∬ F . d S = ∬ x i + y j + 5 k . v i + v j d A

∬ F . d S = ∬ v x + v y d A = ∬ v ( x + y ) d A

Para os pontos em S 2 , nós temos que x + y = 2

∬ F . d S = s ∬ v d A

Como u ∈ ( 0,2 π ) e v ∈ ( 0,1 ) ,

∬ F . d S = 2 ∫ 0 1 ∫ 0 2 π v d u d v = 2 ∫ 0 1 v d v ∫ 0 2 π d u

∬ F . d S = 2 v 2 2 0 1 2 π = 2 π

Passo 5

S 3 é a parte do cilindro limitada pelos planos x + y = 2 e y = 0 . A representação paramétrica de S 3 é

( sen ⁡ u , v , cos ⁡ u )

onde u ∈ ( 0,2 π ) . Como 0 < y < 2 - x , nós temos que 0 < v < 2 - sen ⁡ u . Portanto,

r u = cos ⁡ u i + 0 j - sen ⁡ u k

r v = 0 i + j + 0 k

r u × r v = i j k cos ⁡ u 0 - sen ⁡ u 0 1 0 = sin ⁡ u i + 0 j + cos ⁡ u k

Note que r u × r v está apontando para fora. Assim,

d S = r u × r v d A = sin ⁡ u i + 0 j + cos ⁡ u k   d A

Passo 6

Resolvendo a integral, temos:

∬ F ⋅ d S = ∬ sen ⁡ u i + v j + 5 k ⋅ sin ⁡ u i + 0 j + cos ⁡ u k   d A

Organizando, chegaremos a

∬ sin 2 ⁡ u + 5 cos ⁡ u   d A

onde os nossos limites de integração serão:

u ∈ 0,2 π , 0 < v < 2 - sen ⁡ u

Por isso:

∫ 0 2 π ∫ 0 2 - sen ⁡ u sin 2 ⁡ u + 5 cos ⁡ u   d v d u

Resolvendo de dentro para fora, ou seja, primeiro em relação a d v :

∫ 0 2 π ( sen 2 ⁡ u + 5 cos ⁡ u ) ( 2 - sen ⁡ u ) d u

Guarda bem essa primeira equação aí, vamos chama-la de equação ( 1 ) .

Usando a seguinte propriedade:

∫ a b f x d x = ∫ a b f a + b - x d x

Temos,

∫ 0 2 π sen 2 ⁡ 2 π - u + 5 cos ⁡ 2 π - u 2 - sen ⁡ 2 π - u d u

Organizando, chegaremos a nossa segunda ( 2 ) equação:

∫ 0 2 π ( sen 2 ⁡ u + 5 cos ⁡ u ) ( 2 + sen ⁡ u ) d u

Somando as equações 1 e   ( 2 ) , teremos:

2 ∬ F ⋅ d S = ∫ 0 2 π sin 2 ⁡ u + 5 cos ��� u 4   d u

∬ F ⋅ d S = 2 ∫ 0 2 π sin 2 ⁡ u + 5 cos ⁡ u d u

Organizando,

∬ F ⋅ d S = 2 ∫ 0 2 π 1 2 - cos ⁡ 2 u 2 + 5 cos ⁡ u d u

Calculando e pondo os limites de integração, teremos:

∬ F . d S = 2 u 2 - sin ⁡ 2 u 4 + 5 sin ⁡ u 0 2 π = 2 π

Assim, o fluxo total é igual a:

F l u x o = 0 + 2 π + 2 π = 4 π

Resposta

F l u x o = 4 π

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Calcule a integral de superfície ∫ ∫ SF ∙ d S para o campo vetorial F e superfície orientada S . Em outras palavras, determine o fluxo de F através de S . Para superfícies fechadas, use a orientação p
Calcule a integral de superfície ∫ ∫ SF ∙ d S para o campo vetorial F e superfície orientada S . Em outras palavras, determine o fluxo de F através de S . Para superfícies fechadas, use a orientação p
Calcule a integral de superfície ∫ ∫ SF ∙ d S para o campo vetorial F e superfície orientada S . Em outras palavras, determine o fluxo de F através de S . Para superfícies fechadas, use a orientação p
Calcule a integral de superfície ∫ ∫ SF ∙ d S para o campo vetorial F e superfície orientada S . Em outras palavras, determine o fluxo de F através de S . Para superfícies fechadas, use a orientação p
Calcule a integral de superfície ∫ ∫ SF ∙ d S para o campo vetorial F e superfície orientada S . Em outras palavras, determine o fluxo de F através de S . Para superfícies fechadas, use a orientação p