Enunciado
Cálculo - Cálculo Volume 1 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 3.10 - Ex. 7
Um avião voa horizontalmente a uma altitude de 1 mi, a 500 mi/h, e passa diretamente sobre uma estação de radar. Encontre a taxa segundo a qual a distância do avião até a estação está crescendo quando ele está a 2 mi além da estação.
Passo 1
Opa, bora lá! Vamos analisar o que nosso probleminha está falando.
Bom, ele nos diz que tem um avião voando lindamente a uma altura constante de (como não falou nadica sobre a variação de altitude, vamos considerar constante) e com uma velocidade constante de também (vamos fingir que ele ligou o piloto automático e manteve).
Ele nos diz que o avião passa diretamente por uma estação de radar, e queremos encontrar qual a taxa segundo a qual a distância do avião até a estação cresce quando ele está a da estação.
Vamos fazer um esqueminha para ficar claro!
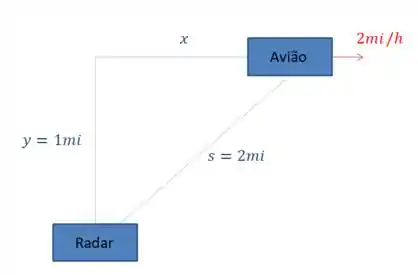
Aqui nos é dado a velocidade horizontal do avião, portanto:
E queremos encontrar a variação da distância do avião com relação ao radar, ou seja, queremos:
Viu, nem é tão difícil assim. Eaii, partiu??
Passo 2
Já vimos que é um triângulo retângulo, então nos resta aplicar o teorema de Pitágoras. Percebe que a distância do avião até o radar é a hipotenusa do triângulo.
Vamos derivar ambos os lados com relação ao tempo.
Resolvendo para que é o que queremos encontrar:
Agora resta substituir uns valores aí.
Passo 3
Sabemos que e que . Resta encontrarmos o valor da posição horizontal quando , para isso, podemos usar a expressão que veio lá de Pitágoras.
Como é uma distância, e só pode ser positiva, temos:
Substituindo na expressão no final do Passo 2, temos:
Prontinho!