Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 3.8 - Ex. 45

Um avião voa horizontalmente a uma altitude de 5   k m e passa diretamente sobre um telescópio no chão. Quando o ângulo de elevação for π 3 , esse ângulo estará diminuindo a uma taxa de π 6 rad/min. Quão rapidamente estará o avião se movendo naquele instante?

Passo 1

Opa, bora resolver esse problema!

Esse enunciado descreve uma situação envolvendo um avião voando horizontalmente a uma altitude de 5   k m e passando diretamente sobre um telescópio no chão. O telescópio está sendo usado para observar o avião, e o ângulo de elevação do telescópio em relação ao avião está diminuindo a uma taxa constante de π 6   r a d / m i n quando o ângulo é π 3   r a d i a n o s .

O enunciado pede para determinar a velocidade do avião nesse instante específico, quando o ângulo de elevação é π 3   r a d i a n o s   e está diminuindo a uma taxa de π 6   r a d / m i n .

Para resolver esse problema, precisamos usar trigonometria e cálculo diferencial. Vamos chamar x da distância horizontal entre o telescópio e o avião, e θ   do ângulo de elevação do telescópio em relação ao avião.

Passo 2

Temos um avião voando a uma altitude de 5   k m quando passa por cima de um telescópio. Se liga no esqueminha:

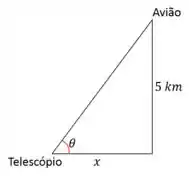
Vamos chamar o deslocamento horizontal do avião de x e o ângulo de inclinação do telescópio de θ .

Logo, a relação entre x e θ é dada por:

tg ⁡ θ = 5 x

Ou

ctg ⁡ θ = x 5

Passo 3

Para derivar a expressão \ ctg ⁡ θ = x 5

Podemos usar a regra da cadeia.

Primeiro, lembramos que cot ⁡ ( θ ) = 1 tan ⁡ θ .

Portanto, cot ⁡ ( θ = 1 tan ⁡ θ

Usando a regra da cadeia, derivamos cos ⁡ θ   em relação a t :

d d t cot ⁡ θ = d d θ cot ⁡ θ ⋅ d θ d t

= - csc 2 ⁡ θ ⋅ θ ' ( t )

- csc 2 ⁡ θ × θ ' t = x ' ( t ) 5

θ ' t = - x ' t × sen 2 ⁡ θ 5

Passo 4

Quando θ = π 3 e está variando a uma razão de θ ' t = - π 6 rad/min então:

- π 6 = - x ' t × sen 2 ⁡ π 3 5

- π 6 = - x ' t × sen 2 ⁡ π 3 5

5 π 6 = x ' t × 3 4

x ' t = 10 π 9

Portanto, a velocidade do avião é de 10 π 9 km/min.

Resposta

A velocidade do avião é de 10 π 9 km/min.

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O lucro de um varejista é $ 100 ⋅ y quando são gastos diariamente $ x em propaganda e y = 2500 + 36 x - 0,2 x 2 Use a derivada para determinar se seria lucrativo aumentar a verba de propaganda, consid
Se R(x) for o rendimento total recebido das vendas de x aparelhos de televisão e R x = 600 x - 1 20 x 3 c) Ache o rendimento real da venda da vigésima primeira televisão.
Uma frente fria aproxima-se de uma região. A temperatura é T graus t horas após a meia-noite e T = 0,1 400 - 40 t + t 20 ≤ t ≤ 4 Ache a taxa de variação média de T em relação a t entre 5h e 6h;
O lucro de um varejista é $ 100 ⋅ y quando são gastos diariamente $ x em propaganda e y = 2500 + 36 x - 0,2 x 2 Use a derivada para determinar se seria lucrativo aumentar a verba de propaganda, consid
A importância no custo total da fabricação de x relógios de uma fábrica é dada por C x = 1500 + 3 x + x 2 Ache a função custo marginal;Ache o custo marginal quando x=40.