Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 3.9 - Ex. 50

O ponteiro dos minutos de um relógio mede 8   m m , enquanto o das horas tem 4   m m de comprimento. Quão rápido está variando a distância entre a ponta dos ponteiros à 1 hora?

Passo 1

Opa, bora resolver essa questão! Temos um relógio onde o ponteiro dos minutos mede 8   m m e o das horas tem 4   m m de comprimento. Assim:

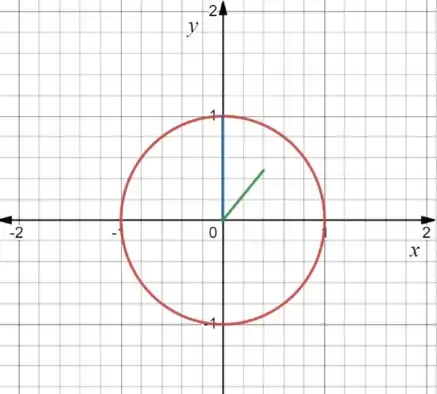
Queremos saber a velocidade que a distância entre a ponta dos ponteiros esta variando quando bate 1 hora!

Vamos alocar esse problema no plano cartesiano de modo que as pontas dos ponteiros são como pontos, o ponteiro dos minutos A = ( x A , y A ) e o ponteiro das horas b B = ( x B , y B ) , o centro da pista é a origem. Logo, seu movimento é descrito por:

A ) Descreve uma circunferência de raio r = 8 mm e velocidade angular de w = 2 π   r a d   m i n . Então:

x A = r cos ⁡ ( w t ) = 8 cos ⁡ 2 π t

y A = r sen ⁡ ( w t ) = 8 sen ⁡ 2 π t

B ) Raio r = 4 mm e velocidade angular de w = 2 π   r a d   60   m i n = π 30 r a d / m i n . Então:

x B = r cos ⁡ ( w t ) = 4 cos ⁡ π t 30

y B = r sen ⁡ ( w t ) = 4 sen ⁡ π t 30

Passo 2

Logo, a distância d entre eles é dada por:

d = x A - x B 2 + y A - y B 2

d = 8 cos ⁡ 2 π t - 4 cos ⁡ π t 30 2 + 8 sen ⁡ 2 π t - 4 sen ⁡ π t 30 2

d = 8 2 1 + 4 2 1 - 64 cos ⁡ 2 π t cos ⁡ π t 30 + cos ⁡ 2 π t cos ⁡ π t 30

Como cos ⁡ a - b = cos ⁡ a   cos ⁡ b   +   sen ⁡ a   sen ⁡ b   então:

d = 80 - 64 cos ⁡ 59 π t 30

d 2 = 80 - 64 cos ⁡ 59 π t 30

Passo 3

Derivando em função do tempo em minutos:

2 d × d ' t = 64 sen ⁡ 59 π t 30 × 59 π 30

d ' t = 32 sen ⁡ 59 π t 30 × 59 π 30 d

d ' t = 32 sen ⁡ 59 π t 30 × 59 π 30 80 - 64 cos ⁡ 59 π t 30

Quando o relógio marca 1 hora, o ponteiro dos minutos está no 12 ( 90 ° ) e o das horas está no 1 ( 60 ° ) temos:

x A = 8 cos ⁡ 90 ° = 0

y A = 8 sen ⁡ 90 ° = 8

x B = 4 cos ⁡ 60 ° = 2

y B = 4 sen ⁡ 60 ° = 2 3

E sua distância é:

d = 0 - 2 2 + 8 - 2 3 2

d = 80 - 32 3

Então:

d 2 = 80 - 64 cos ⁡ 59 π t 30

80 - 32 3 = 80 - 64 cos ⁡ 59 π t 30

3 = 2 cos ⁡ 59 π t 30

cos ⁡ 59 π t 30 = 3 2 = cos ⁡ 30 °

Então, a variação da distância:

d ' t = 32 sen ⁡ 30 ° × 59 π 30 80 - 64 cos ⁡ 30 °

d ' t = 16 × 59 π 30 80 - 32 3

d ' t = 16 × 59 π 30 80 - 32 3 = 19,94

Logo, nesse momento a distância varia a uma taxa de aproximadamente 19,94 mm/min.

Resposta

Nesse momento a distância varia a uma taxa de aproximadamente 19,94 mm/min.

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Se a água estiver sendo drenada de uma piscina e V litros for o volume de água na piscina t min após começar o escoamento, onde V = 250 ( 1600 - 80 t + t 2 ) Ache a taxa média segundo a qual a água de
Nos Exercícios de 33 a 35, use o conceito de taxa relativa, definido como segue se y = f(x), a taxa relativa da variação de y com relação a x em x1 é dada por f ' x 1 f x 1 ou, equivalentemente, dy /
Estima-se que um empregado de uma firma que faz molduras para quadros possa pintar y molduras x horas, após começar o trabalho às 8 horas da manhã e y = 3 x + 8 x 2 - x 30 ≤ x ≤ 4 b) Ache o número de
Se a água estiver sendo drenada de uma piscina e V litros for o volume de água na piscina t min após começar o escoamento, onde V = 250 ( 1600 - 80 t + t 2 ) b) Ache o quão rápido a água está fluindo
Nos Exercícios de 33 a 35, use o conceito de taxa relativa, definido como segue se y = f(x), a taxa relativa da variação de y com relação a x em x1 é dada por f ' x 1 f x 1 ou, equivalentemente, dy /