Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 3.9 - Ex. 44

Um farol está localizado em uma pequena ilha, e a distância entre ele e o ponto P   mais próximo dele em uma costa reta do continente é de 3   k m . Sua luz gira quatro revoluções por minuto. Quão rápido estará se movendo o feixe de luz ao longo da costa quando ele estiver a 1   k m de P ?

Passo 1

Fala aí, pessoal! 😬

Nesse problema temos um farol que gira a 4   r e v / m i n e nosso objetivo é determinar a velocidade do feixe de luz a 1 k m de P sendo que P está a 3   k m de distância.

Tem ideia de como fazemos isso? 👀

Vamos chamar de θ o ângulo descrito entre a perpendicular à costa e o ponto em que está incidindo o feixe de luz e nomear como x a distância entre o ponto P em que está incidindo o feixe de luz então, temos a seguinte situação:

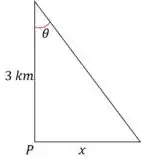
Logo, a relação entre θ e x é:

tg ⁡ θ = x 3

Veja só! 😉

Passo 2

Agora, vamos derivar para correlacionar as taxas de variação:

sec 2 ⁡ θ × θ ' t = x ' ( t ) 3

θ ' t = x ' t × cos 2 ⁡ θ 3

Como o cosseno é o cateto adjacente sobre a hipotenusa, e a hipotenusa é a raiz da soma dos quadrados dos catetos, temos:

cos ⁡ θ = 3 x 2 + 3 2

Então, a derivada é:

θ ' t = x ' t × 3 x 2 + 3 2 2 3

θ ' t = 3 x ' t x 2 + 9

x ' t = ( x 2 + 9 )   θ ' t 3

A θ deve estar em radianos, consequentemente, a taxa com que esse ângulo varia deve estar em radianos por unidade de tempo. Vamos escolher a unidade de tempo como horas.

Tranquilo até aqui? 😎

Passo 3

Se o farol gira quatro revoluções por minuto e cada revolução temos 2 π radianos e um minuto é 1 60 de hora, então:

θ ' t = 4 r e v m i n = 4 2 π   r a d 1 60   h o r a = 480 π   r a d / h o r a

Logo, a taxa com que x varia, quando x = 1   k m é:

x ' t = x 2 + 9 θ ' t 3

x ' t = 1 2 + 9 480 π 3

x ' t = 1600 π

Logo, a taxa com que o feixe de luz está se movendo é de 1600 π km/h.

E aí! O que achou? Responde Aí! 😇

Resposta

A taxa com que o feixe de luz está se movendo é de 1600 π km/h.

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma partícula desloca-se sobre o eixo x com função de sua posição x = 3 + 2 t - t 2 , t ≥ 0 .a) Qual a velocidade no instante t ?b) Qual a aceleração no instante t ?c) Estude a variação do sinal de v
A equação do movimento de uma partícula que se desloca ao longo do eixo x é x = e - t sen ⁡ t , t ≥ 0 .a) Determine a velocidade e a aceleração no instante t .b) Calcule lim t → + ∞ ⁡ e - t sen ⁡ t .c
A posição de uma partícula que se desloca ao longo de eixo x varia com o tempo segundo a equação x = v 0 k 1 - e - k t , t ≥ 0 , em que v 0 e k são constantes estritamente positivas.a) Qual a velocida
Suponha que os comprimentos dos segmentos A B e 0 B sejam, respectivamente, 5c m e 3c m . Suponha, ainda, que θ esteja variando a uma taxa constante de 1 2 rad/s. Determine a velocidade de A , quando
A posição de uma partícula que se desloca ao longo de eixo x depende do tempo de acordo com a equação x = - t 3 + 3 t 2 , t ≥ 0 .a) Estude o sinal de v t .b) Estude o sinal de a t .c) Calcule lim t →