Enunciado
Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 6.6 - Ex. 22
Um balde de contendo de água está pendurado na ponta de uma corda de que pesa . A outra extremidade da corda está presa em uma roldana. Qual é o trabalho requerido para içar toda a corda para cima, enrolando-a na roldana, se a corda for içada a uma taxa de e se, enquanto o balde for içado, a água vaza do balde a uma taxa de ?
Passo 1
Vamos usar nossa criatividade para interpretar esse problema. Temos essa situação:
Queremos o trabalho para içar toda a corda. Podemos cortar nosso comprimento da corda em fatias bem fininhas e considerar que a força para mover uma fatia é constante e deve superar a força peso.
Aí lembramos que para uma força constante:
Para descobrimos o trabalho total, devemos somar o trabalho realizado em cada fatia.
Mas a gente lembra que tem um balde com água também, que vai perdendo massa, ou seja, a força peso dele vai variando. E se a gente tem uma força que varia:
Para achar o trabalho requerido, devemos somar o trabalho realizado em na corda e no balde. Vamos lá!
Passo 2
Vamos descobrir o valor da força por fatia.
Já que nossas fatias são bem finas, podemos dizer que elas têm um comprimento infinitesimal .
Para achar a massa, podemos multiplicar o comprimento pela densidade de massa da corda que é igual a .
E como queremos que a força por fatia supere a força peso:
Passo 3
Precisamos entender agora como é o nosso valor de para cada fatia:
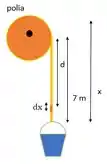
Repara que podemos escrever:
Sendo que vai de a.
Passo 4
O trabalho fica com essa carinha:
Mas queremos o trabalho total. Lembra que integrar também é calcular somatório:
Passo 5
Vamos pensar agora no trabalho para levantar o balde:
A gente quer levantar ele de para . Mas quem é ?
O enunciado diz que a taxa de variação da altura é , enquanto a taxa de variação da massa do balde é . Se dividimos esses valores um pelo outro a gente a acha a taxa de variação da massa pela altura:
Podemos escrever assim uma expressão para a massa do balde em função de :
Passo 6
Agora só calcular a integral:
E calculando o trabalho total: