Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 8.3 - Ex. 16

Uma barragem está inclinada a um ângulo de 30 º da vertical e tem o formato de um trapézio isósceles de 100 pés de largura no topo e 50 pés no fundo e um lado inclinado de 70   pés. Calcule a força hidrostática na barragem quando ela estiver cheia de água.

Passo 1

Com o enunciado dado a gente consegue esboçar a seguinte figura:

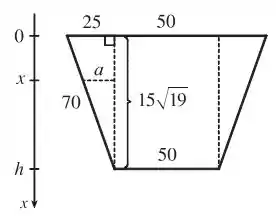
Sabendo que o topo tem 100 m de largura, a gente consegue dizer que a base dos triângulos retângulos formados tem 25 m . Assim, conseguimos achar a altura lembrando um pouquinho de trigonometria, que é

h = 70 2 - 25 2 cos ⁡ 30 °

h = 15 19 3 2 m

Agora a gente acha a largura do trapézio menor. Pela figura fica fácil de ver, que é w = 50 + 2 a . Por semelhança de triângulos, temos

25 h = a h - x → a = 25 h h - x

Assim, nosso valor de w é

w = 50 + 2 25 h h - x = 50 + 50 h h - 50 h x = 50 + 50 - 50 x h = 100 - 50 x h

Passo 2

Agora aproximamos um pouco mais esse triângulo retângulo para analisarmos melhor:

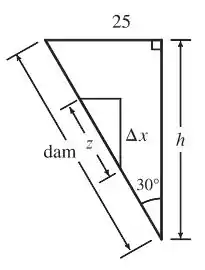
Olhando essa figura, a gente consegue ver que cos ⁡ 30 ° = ∆ x z → z = ∆ x sec ⁡ 30 ° = 2 ∆ x / 3 .

Passo 3

Agora bora calcular a força!

F = ∫ 0 h δ x 100 - 50 x h 2 3 d x =   2 00 δ 3 ∫ 0 h x d x -   1 00 δ h 3 ∫ 0 h x 2 d x = 200 δ 3   h 2 2 - 100 δ h 3 h 3 3 =

200 δ h 2 3 3 = 200 62.5 3 3 12,825 4 ≈ 7.71 × 10 6 l b  

Resposta

7.71 × 10 6 l b .

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

31.O topo de um tanque tem 3m de comprimento e 2m de largura. As extremidades são triângulos equiláteros verticais, com um vértice apontado para baixo. Qual a força total em uma extremidade, quando el
Nos exercícios 27 a 30 , temos uma comporta de uma represa, colocada verticalmente, com a forma indicada.Calcular a força total contra a comporta30.Um trapézio isósceles com 17m de largura e 9m na bas
Nos exercícios 27 a 30 , temos uma comporta de uma represa, colocada verticalmente, com a forma indicada.Calcular a força total contra a comporta28.Um trapézio isósceles com 30m de largura e 20m de la
Em cada parte, monte, mas não calcule, uma integral que resolva o problema.(a) Encontre a força que um fluido exerce sobre o lado de uma caixa que tem base quadrada com 3 m de lado e está cheia até um
Enuncie uma fórmula integral para a força fluida F exercida sobre uma superfície plana verticalmente submersa em um fluido de peso específico ρ e use somas de Riemann para derivar a fórmula dada.