Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 4.7 - Ex. 57
Qual é o menor comprimento de um segmento de reta que é cortado pelo primeiro quadrante e é tangente à curva em algum ponto?
Passo 1
Fala, galera! Beleza? Vamos resolver essa questão!
O enunciado pediu pra gente determinar qual é o menor comprimento de um segmento de reta que é cortado pelo primeiro quadrante e é tangente à curva em algum ponto.
E a ideia para resolver esse exercício será esboçar esse segmento de reta com as características dada para então descobrir uma expressão para seu comprimento.
Depois usaremos a derivada para minimizar seu tamanho.
Passo 2
Podemos começar usando as informações dadas pelo enunciado.
Sabemos que o segmento de reta é cortado pelo primeiro quadrante. Isso significa que ele possui valores se e positivos.
Além disso, sabemos que ele é tangente a curva Então podemos desenhar essa curva e colocar o segmento a tangenciando.
Esboçando isso em um gráfico, teremos mais ou menos isso aqui:
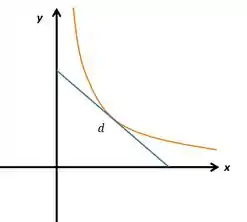
Repare que precisamos encontrar o tamanho desse segmento de reta . Como ele é tangente a curva em um ponto, podemos escrever esse ponto da seguinte maneira:
Mas para traçarmos uma reta tangente a esse ponto precisamos achar o coeficiente angular, que nada mais é que a derivada da função no ponto. Então, vamos derivar , substituir . Em seguida, vamos usar Pitágoras para calcular o tamanho da reta , assumindo um triângulo retângulo ali no gráfico e minimizar a função encontrada através do teste da primeira derivada.
Vamos lá!
Passo 3
Vamos começar derivando em relação a .
Essa derivação é feita usando a regra do expoente. Já que pode ser escrita com:
Assim,
Ou melhor:
E para o ponto , temos:
Então, usando a equação geral da reta () no ponto , temos o seguinte:
Logo, a nossa reta tangente à curva é:
Observe que o ponto de interseção com o eixo é e o ponto de interseção com o eixo é obtido fazendo , de modo que teremos:
Passo 4
Agora vamos achar o comprimento da reta, usando a relação de Pitágoras:
Elevando os termos ao quadrado:
Mas a gente quer q o menor comprimento do segmento de reta, então precisamos minimizar . Pra isso, basta minimizarmos o que está dentro da raiz. Assim,
Derivando através da regra do expoente novamente, teremos:
Igualando a 0 para achar os pontos críticos:
E isolando :
Portanto,
pois estamos no 1° quadrante.
Passo 5
Agora é só conferir se isso é um ponto de mínimo mesmo. Para isso podemos usar o teste da segunda derivada.
Para , vemos que ponto de mínimo. Agora vamos substituir na expressão para . Assim, temos:
Portanto, o menor comprimento de um segmento de reta é .
Valeu, galera! Até a próxima! 😉