Enunciado
Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 6.7 - Ex. 22
A face de um reservatório adjacente à agua é inclinado 45º em relação a vertical . A face é um retângulo com 80m de comprimento e um lado inclinado de 40m. Se o reservatório está cheio, ache a força total sobre a face , em decorrência da pressão da agua.
Sugestão : Resolva usando F =
Passo 1
Desenhando o problema
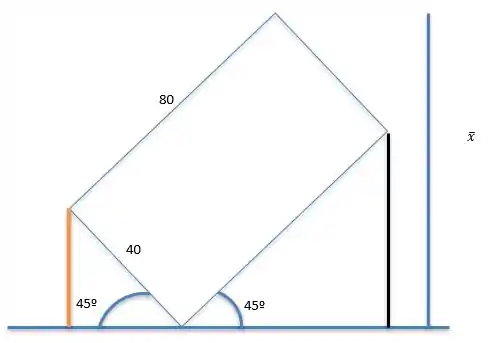
Temos que é uma composição, soma do segmento de reta preto e laranja.
Olhando para o segmento laranja ( X1) , vemos que ele faz parte de um triangulo com hipotenusa 40 e ângulo de 45º. Logo ele pode ser calculado como sen45 = X1/40
Logo X1 = 40sen45
O mesmo vale para o segmento preto (X2), logo : sen45 = X2/80
X2 = 80sen45
Assim
Passo 2
Calculando F:
F =
Sabendo que
da agua = 1000 kg/m³
g = 10m/s²
Logo : F = onde é a altura do objeto mergulhado.
F = 10³ . 10 .
Resposta
F =27