Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 6.2 - Ex. 58
58. A base de é a região delimitada pela parábola e pelo eixo . As secções transversais perpendiculares ao eixo são quadradas.
Passo 1
Fala aí, pessoal! 😁
Nesse problema queremos encontrar o volume do sólido delimitado pela parábola e o eixo sendo as secções transversais perpendiculares ao eixo quadradas...
Tem ideia de como fazemos isso? 🤔
Vamos visualizar a região descrita:
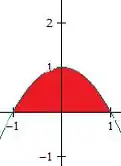
Essa é a base do nosso sólido. As secções transversais dele são quadrados e perpendiculares ao eixo , de lado .
Bora lá! 😉
Passo 2
A área do quadrado é:
E o volume do sólido é:
Simplificando...
E aí! O que achou? Responde Aí! 😁
Resposta
Exercícios de Livros Relacionados
Use camadas cilíndricas para encontrar o volume do sólido que resulta quando a região englobada pelas curvas gira em torno do eixo y . y = 2 x - x 2 , y = 0
Determine se a afirmação dada é verdadeira ou falsa. Explique sua resposta.A aproximação das somas de Riemann V ≈ ∑ k = 1 n 2 π x k nf x k n Δ x ko n d ex k n = x k + x k - 1 2 para o volume de um sól
( a ) Use camadas cilíndricas para encontrar o volume do sólido que é gerado quando a região sob a curva y = x 3 - 3 x 2 + 2 x e acima de [ 0 ,1 ] gira em torno do eixo y . ( b ) Para esse problema, o
Usando o método das camadas cilíndricas, monte uma integral (mas não a calcule) para o volume do sólido gerado quando a região R é girada em torno ( a ) da reta x = 1 e ( b ) da reta y = - 1 . R é a r
Determine se a afirmação dada é verdadeira ou falsa. Explique sua resposta.No método das camadas cilíndricas, a integração é efetuada num intervalo do eixo de coordenadas que é perpendicular ao eixo d