Exercícios de Cálculo de Volume pelas Seções Transversais - Lista de Exercícios Resolvida
Questão 1
Dexter estava tomando sorvete quando de repente sentiu uma vontade enorme de saber o volume da casquinha. Tendo ela de altura e sendo composta por dois cone, um exterior com de raio e outro interior com de raio inscrito ao primeiro, ache o volume pro Dexter enquanto ele come.

Dica: o interior do cone menor é oco
Ver solução completaQuestão 2
Encontre o volume do sólido cuja base é a região delimitada pelas curvas e cujas seções transversais perpendiculares ao eixo são quadrados
Ver solução completaQuestão 3
Calcule o volume do sólido de revolução abaixo usando Cálculo de Volumes por Seções Transversais. O sólido foi feito girando a curva em torno do eixo .
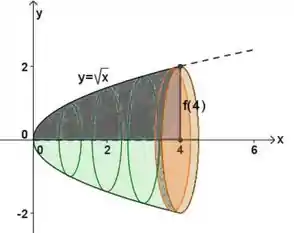
Questão 4
Deduza o volume de uma esfera usando Cálculo de Volumes por Seções Transversais.
Ver solução completaQuestão 5
Considere um sólido com base circular de raio . As secções transversais paralelas, perpendiculares à base são triangulares. Triângulos estes, isósceles com medidas de base e altura iguais. Encontre o volume deste sólido.
Ver solução completaQuestão 6
Uma cunha curva é obtida através de um corte perpendicular ao eixo de um cilindro, seguido de um corte que cruza o eixo formando um ângulo de , conforme a figura:
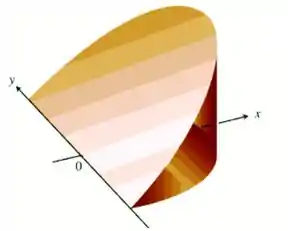
Sabendo que o cilindro possuía raio , antes de ser cortado, calcule o volume da cunha.
Ver solução completaQuestão 7
Encontre o volume do sólido cuja base é a região parabólica
e cujas seções transversais perpendiculares ao eixo são quadradas.
Ver solução completaQuestão 8
Dois cilindros circulares retos de raio r têm eixos que se intersectam em ângulos retos. Encontre o volume do sólido comum a ambos (Sugestão: Um oitavo do sólido está esboçado na figura abaixo).
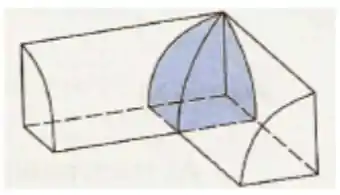
Questão 9
Sólido do primeiro octante, delimitado pelos planos , pela esfera , situado entre os cones e
Ver solução completaQuestão 10
O volume de um certo sólido é dado por
Em relação ao problema anterior, exprima o mesmo volume como uma integral tripla em coordenadas cilíndricas.
Ver solução completaQuestão 11
Fez-se um orifício circular em uma esfera, de forma que o eixo do orifício coincidiu com o diâmetro da esfera. Calculou-se o volume do sólido restante e obteve-se
Determine o raio do orifício, o raio da esfera e o Valor de .
Ver solução completaQuestão 13
Calcule o volume do sólido do primeiro octante, limitado pelas superfícies , , , , e .
(Sugestão: Faça e )
Ver solução completaQuestão 15
Calcule o volume do sólido limitado pelo plano , pelo cilindro e pelo cone .
Ver solução completaQuestão 16
Ao calcular-se, por dupla integração, o volume do sólido situado abaixo da superfície de equação e acima de uma região do plano , obteve-se a seguinte soma de integrais
Qual é esse sólido? É possível obter o valor do mesmo volume sem a necessidade do cálculo de uma soma de integrais? Qual o valor do volume?
Ver solução completaQuestão 17
Determine o volume dos sólidos S, usando integração.
b) um cone truncado de base circular.

Questão 18
Para cada uma das funções abaixo, seja a região entre o gráfico das funções e o eixo e o sólido obtido pela rotação desta região em torno do eixo . Calcule os volumes dos sólidos obtidos
Ver solução completaQuestão 19
Para cada uma das funções abaixo, seja a região entre o gráfico das funções e o eixo e o sólido obtido pela rotação desta região em torno do eixo . Calcule os volumes dos sólidos obtidos
Ver solução completaQuestão 20
Seja a a região limitada entre os gráficos e . Seja o sólido obtido girando esta região em torno do eixo . Qual o volume de ?
Ver solução completaQuestão 21
Encontre o volume do solido obtido pela rotação da região delimitada por baixo pelo gráfico de e por cima pela curva , em torno do eixo . Esboce a região, o sólido obtido e uma ‘seção’ típica
Ver solução completaQuestão 22
Seja , com . Calcule o valor médio de e encontre uma boa aproximação para tal que . (ou seja, determine a altura do
caixote que usaremos para guardar a região abaixo do gráfico de ).
Ver solução completaQuestão 24
Encontre o volume do solido obtido pela rotação em torno do eixo da região entre as curvas e . Esboce o solido e a região
Ver solução completaQuestão 26
Calcule o volume limitado pelo parabolóide , pelo plano e pelos cilindros e .
Ver solução completaQuestão 27
Calcule o volume limitado pelo parabolóide , pelo cilindro e pelo plano .
Ver solução completaQuestão 28
Calcule o volume do sólido contido no parabolóide , limitado por este e pela esfera de equação .
Ver solução completaQuestão 30
Determine o volume do sólido que está acima do cone e abaixo da esfera .
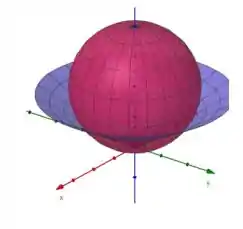
Questão 31
Encontre o volume do sólido que permanece depois que um furo circular de um raio é perfurado através do centro de um esfera sólida de raio por:
- Seções transversais
Questão 32
Seja a área o conjunto de pontos tais que , , e .
- Determine o volume gerado pela revolução da área em torno da reta ;
- Determine o volume gerado pela revolução da área em torno da reta .
Questão 33
A base de é uma região elíptica delimitada pela curva . As secções transversais perpendiculares ao eixo são triângulos isósceles retos com hipotenusa na base
Ver solução completaQuestão 35
Determine o volume da região E limitada pelos cilindros e pelos cones ,
Ver solução completaQuestão 36
Seja a área o conjunto de pontos tais que , , e .
- Determine o volume gerado pela revolução da área em torno da reta ;
- Determine o volume gerado pela revolução da área em torno da reta .
Questão 37
Calcule o volume do sólido obtido pela rotação em torno da reta da região delimitada pelas
parábolas
Ver solução completaQuestão 38
Determine o volume do sólido obtido pela rotação em torno do eixo do conjunto
Questão 39
Considere um sólido com base circular de raio . As secções transversais paralelas, perpendiculares à base são triangulares. Triângulos estes, isósceles com medidas de base e altura iguais. Encontre o volume deste sólido.
Ver solução completaQuestão 40
Formule a integral que calcula o volume do sólido obtido ao girar a região limitada pelas curvas , , e ao redor do eixo apontado:
b) ao redor do eixo
Ver solução completaQuestão 41
Formule a integral que calcula o volume do sólido obtido ao girar a região limitada pelas curvas , , e ao redor do eixo apontado:
c) ao redor do eixo
Ver solução completaQuestão 42
Considere a região delimitada pela curva e pelas retas e :
Esboce a região .
Determine o volume do sólido obtido pela rotação da região ao redor da reta .
Ver solução completaQuestão 43
Formule a integral que calcula o volume do sólido obtido ao girar a região limitada pelas curvas , , e ao redor do eixo apontado:
a) ao redor do eixo
Ver solução completaQuestão 44
Formule a integral que calcula o volume do sólido obtido ao girar a região limitada pelas curvas , , e ao redor do eixo apontado:
d) ao redor do eixo
Ver solução completaQuestão 46
Encontre o volume obtido pela rotação em torno do eixo da curva: , . (Dica: Coloque em evidência)
Ver solução completaQuestão 47
Determine o volume do sólido obtido pela rotação em torno do eixo do conjunto
Questão 48
Encontre o volume do sólido delimitado superiormente pelo paraboloide e inferiormente pelo quadrado
Ver solução completaQuestão 49
Encontre o volume do sólido que está abaixo do paraboloide elíptico e acima do retângulo
Ver solução completaQuestão 50
Determine o volume dos sólidos S, usando integração.
c) uma calota esférica
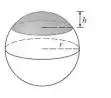
Questão 51
Determine o volume dos sólidos S, usando integração.
e) a região delimitada por dois cilindros circulares retos que se interceptam perpendicularmente.
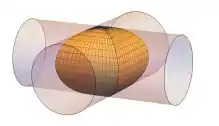
Questão 52
Ache o volume comum a duas esferas de raio r se o centro de cada esfera está na superfície da outra.
Ver solução completaQuestão 53
Seja a região limitada verticalmente por e , e lateralmente por . Esboce a região e calcule seu volume.
Ver solução completaQuestão 54
Calcule o volume do sólido no semiespaço , delimitado pelo cilindro e pelos planos e .
Ver solução completaQuestão 55
Calcule a massa do sólido limitado pelo cone e pelo plano ; se a densidade de massa e dada por .
Ver solução completaQuestão 57
Determine o volume do sólido limitado pela superfície e os planos , ,
Ver solução completaQuestão 58
Determine o volume do sólido em cada um dos seguintes casos:
e) é a região do primeiro octante limitada pelo cilindro e pelos planos , e .
Ver solução completaQuestão 59
Determine o volume dos sólidos S, usando integração.
- Um cone circular reto de altura h e base r
Questão 60
Uma piscina tem formato circular de raio e profundidade variando linearmente de sul a norte,
sendo que no extremo sul é de e no extremo norte é de . Calcule o volume da piscina.
Ver solução completaQuestão 61
Determine o volume do sólido em cada um dos seguintes casos:
f) é limitado pelos cilindros e , onde .
Ver solução completaQuestão 62
Determine o volume do sólido em cada um dos seguintes casos:
a) é limitado superiormente pelo paraboloide , inferiormente pelo plano e sua projeção no plano é a região limitada por e .
Ver solução completaQuestão 63
Determine o volume do sólido em cada um dos seguintes casos:
b) é limitado superiormente pelo paraboloide , inferiormente pelo plano e sua projeção no plano é o triângulo de vértices , e .
Ver solução completaQuestão 64
Determine o volume do sólido em cada um dos seguintes casos:
c) é a região do primeiro octante limitada pelo cilindro e pelo plano .
Ver solução completaQuestão 65
Determine o volume do sólido em cada um dos seguintes casos:
d) é limitado pelos planos , , e .
Ver solução completaQuestão 66
Dados os gráficos de , e as 5 regiões A1,A2,A3,A4 e A5, delimitadas de acordo com a figura anexa, formule, em cada caso, a integral que calcula o volume do sólido obtido ao girar a região indicada ao redor do eixo apontado
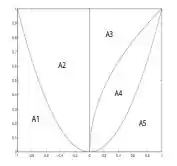
(d) Formule uma integral que calcula a área A4 usando equações paramétricas.
Ver solução completaQuestão 67
Dados os gráficos de , e as 5 regiões A1,A2,A3,A4 e A5, delimitadas de acordo com a figura anexa, formule, em cada caso, a integral que calcula o volume do sólido obtido ao girar a região indicada ao redor do eixo apontado
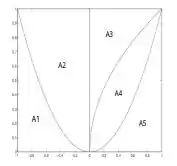
(a)A5 ao redor da reta x = 1 .
Ver solução completaQuestão 68
Dados os gráficos de , e as 5 regiões A1,A2,A3,A4 e A5, delimitadas de acordo com a figura anexa, formule, em cada caso, a integral que calcula o volume do sólido obtido ao girar a região indicada ao redor do eixo apontado
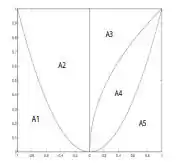
(b)A4 ao redor de x = 2
Ver solução completaQuestão 69
Calcule, utilizando coordenadas cilíndricas, o volume do sólido , limitado abaixo pelo plano e acima pela esfera
Ver solução completaQuestão 70
Calcule, utilizando coordenadas esféricas, o volume do sólido , limitado abaixo pelo plano e acima pela esfera
Ver solução completaQuestão 72
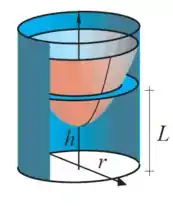
Considere um recipiente cilíndrico de raio , inicialmente em repouso com água até a altura . Em seguida, o recipiente começa a girar até que, juntamente com a água, alcance uma velocidade angular constante igual a . Nesse caso, a superfície da água corresponde à rotação, em torno do eixo , do gráfico de uma função , com . Não havendo perda de água, pode-se mostrar que , onde é a aceleração da gravidade e é uma constante que depende de .
O volume do sólido de rotação do gráfico de em torno do eixo é igual a Use essa informação para calcular o volume de água no recipiente em termos de e .
Usando o item anterior, obtenha como função .
Determine o valor de para que seja igual à metade da altura da água em repouso.
Questão 73
Calcule o volume obtido ao girar a região limitada pelas curvas dadas em torno do eixo :
b) , . ;
Ver solução completaQuestão 74
Calcule o volume obtido ao girar a região limitada pelas curvas dadas em torno do eixo :
d) , . ;
Ver solução completaQuestão 75
Calcule o volume obtido ao girar a região limitada pelas curvas dadas em torno do eixo :
c) , . ;
Ver solução completaQuestão 76
Encontre o volume do sólido obtido pela rotação da região delimitada pelas curvas dadas em torno das retas especificadas.
b) , ; em torno do eixo .
Ver solução completaQuestão 77
Encontre o volume do sólido obtido pela rotação da região delimitada pelas curvas dadas em torno das retas especificadas.
d) , , em torno do eixo .
Ver solução completaQuestão 78
Encontre o volume do sólido obtido pela rotação da região delimitada pelas curvas dadas em torno das retas especificadas.
a) , , , ; em torno do eixo .
Ver solução completaQuestão 79
Dados os gráficos de , e as 5 regiões A1,A2,A3,A4 e A5, delimitadas de acordo com a figura anexa, formule, em cada caso, a integral que calcula o volume do sólido obtido ao girar a região indicada ao redor do eixo apontado
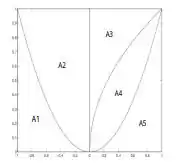
(c) (A2∪A3) ao redor de y = 1.
Ver solução completaQuestão 80
Encontre o volume do sólido obtido pela rotação da região delimitada pelas curvas dadas em torno das retas especificadas.
c) , , , ; em torno do eixo .
Ver solução completaQuestão 81
Responda os itens com respeito à integral
- Utilize a fórmula de integração por partes fazendo e e determine o valor da integral.
- Utilize a fórmula de integração por partes fazendo e e comente por que essa escolha não é boa.
- A integral representa o volume de um sólido gerado pela revolução de uma região, em torno do eixo . Descreva as curvas que delimitam essa região no plano.
Questão 82
Considere o sólido delimitada pelas superfícies Faça um esboço do sólido, mostre a região de integração e
- Formule (mas não resolva) uma integral dupla para calcular o volume do sólido.
- Formule (mas n ̃ao resolva) uma integral tripla para calcular o volume do sólido.
Questão 84
Seja R a região limitada pelos gráficos de e para e S o solido obtido pela revolução desta área em torno do eixo y.
- Calcule o volume de S.
Questão 86
(4) Utilize o Teorema de Pappus-Guldin para determinar:
(b) o volume do sólido de revolução gerado pela rotação do triangulo com vértices nos pontos , , ao redor do eixo .
Ver solução completaQuestão 88
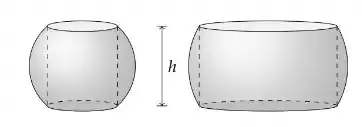
Um anel esférico é o sólido que permanece após a perfuração de um buraco cilíndrico através do centro de uma esfera sólida. Se a esfera tem raio R e o anel esférico tem altura h, prove o fato notável de que o volume do anel depende de h, mas não de R.
Questão 89
Determine o volume do sólido no primeiro octante, delimitado pelos planos coordenados, pelo plano e pela superfície , para .
Ver solução completaQuestão 90
Esboce e calcule o volume do sólido descrito.
c) O sólido cuja base é o semicírculo , cujas secções perpendiculares ao eixo são triângulos equiláteros.
Ver solução completaQuestão 91
Esboce e calcule o volume do sólido descrito.
d) O sólido cuja base é a região elíptica e cujas secções perpendiculares ao eixo são semicírculos.
Ver solução completaQuestão 92
Esboce e calcule o volume do sólido descrito.
e) O sólido cuja base é a região delimitada pela parábola e pelo eixo , e cujas secções perpendiculares ao eixo são quadrados.
Ver solução completaQuestão 93
Esboce e calcule o volume do sólido descrito.
b) Uma pirâmide de altura e base retangular de lados e .
Ver solução completaQuestão 94
5. Calcule o volume do sólido limitado inferiormente pelo cone , de equação , e superiormente pelo paraboloide , de equação
Ver solução completaQuestão 95
Nos exercícios 05 a 12, calcule o volume do sólido descrito em cada caso, usando integração tripla.
Sólido do primeiro octante, delimitado pelos planos coordenados, pelos planos coordenados, pelo plano e pelo cilindro
Ver solução completaQuestão 96
Nos exercícios 05 a 12, calcule o volume do sólido descrito em cada caso, usando integração tripla.
Sólido do primeiro octante, delimitado pelos planos , e pelo cilindro
Ver solução completaQuestão 97
Nos exercícios 05 a 12, calcule o volume do sólido descrito em cada caso, usando integração tripla.
Sólido interior ao cilindro , sendo delimitado pela esfera e pelo plano .
Ver solução completaQuestão 98
Nos exercícios 05 a 12, calcule o volume do sólido descrito em cada caso, usando integração tripla.
Sólido interseção dos paraboloides e .
Ver solução completaQuestão 99
Nos exercícios 05 a 12, calcule o volume do sólido descrito em cada caso, usando integração tripla.
Sólido continho no coze , limitado pela esfera .
Ver solução completaQuestão 100
Nos exercícios 05 a 12, calcule o volume do sólido descrito em cada caso, usando integração tripla.
Sólido interseção da esfera x² + y² + z² = 2com o paraboloide , interior a este.
Ver solução completaQuestão 101
9.7 Seja a região entre os gráficos de e . Seja o sólido obtido girando em torno do eixo e o sólido obtido girando em torno do eixo . Calcule os volumes de e de.
Ver solução completaQuestão 102
O volume de um certo sólido é dado por
Descreva o sólido graficamente, dando as equações das superfícies que o delimitam.
Ver solução completaQuestão 103
10.8 Encontre o volume do sólido obtido pela rotação em torno do eixo da região limitada pelas curvas e .
Ver solução completaQuestão 104
Para cada uma das funções abaixo, seja a região entre o gráfico das funções e o eixo e o sólido obtido pela rotação desta região em torno do eixo . Calcule os volumes dos sólidos obtidos
Ver solução completaQuestão 105
Calcule o volume do sólido obtido quando fazemos a rotação no eixo da região entre o gráfico de e o eixo , com ].
Ver solução completaQuestão 106
Determine o volume do sólido obtido pela rotação em torno do eixo do conjunto
Questão 110
O volume da região limitada pelo cone e pelo cilindro com , pode ser calculado usando coordenadas cilíndricas por
Ver solução completaQuestão 111
Determine o volume do sólido obtido pela rotação em torno do eixo do conjunto
Questão 112
Considere o sólido gerado pela rotação, em torno do eixo , da região limitada pela parábola e a reta , com . Determine o valor de se o volume deste sólido é .
Ver solução completaQuestão 113
Suponha que dois ciclistas estão correndo com a mesma velocidade escalar, ambos partindo, ao mesmo tempo, do ponto . Sabendo que o ciclista percorre o arco de circunferência e o ciclista percorre o arco da curva para . Qual deles chegará primeiro ao ponto ?
Ver solução completaQuestão 114
Determine o volume do sólido gerado pela rotação, em torno do eixo , da região limitada pela curva e pelas retas , e .
Ver solução completaQuestão 115
Para cada , seja a região limitada pelo gráfico de , o eixo e a reta . Se é o volume obtido girando em torno do eixo , e é o volume do sólido obtido girando-se em torno do eixo , determine .
Ver solução completaQuestão 116
Encontre o volume do sólido obtido pela rotação, em torno do eixo , da região infinita situada entre o gráfico de e sua assíntota horizontal.
Ver solução completaQuestão 117
Calcule o volume do sólido obtido pela rotação, em torno da reta , da região limitada pelas curvas e , para .
Ver solução completaQuestão 118
Seja a região infinita delimitada pelas curvas e , . Calcule o volume do sólido obtido pela rotação de em torno do eixo .
Ver solução completaQuestão 119
Calcule o volume do solido obtido pela rotação da região limitada pelas curvas e , em torno do eixo x, no intervalo [0,1].
Ver solução completaQuestão 121
Nos exercícios 05 a 12, calcule o volume do sólido descrito em cada caso, usando integração tripla.
Sólido contido no cone , limitado pela esfera de centro (0, 0, 2) e raio 2.
Ver solução completa