Use camadas cilíndricas para encontrar o volume do sólido que resulta quando a região englobada pelas curvas gira em torno do eixo .
,
Passo 1
Bom galera, a nossa área da integral vai ser:
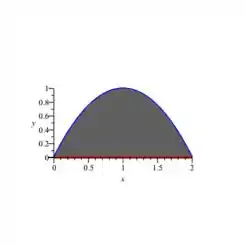
Passo 2
Belezinha, agora a nossa integral para encontrarmos o volume é:
Passo 3
Por fim, a gente só resolve essa integral e pronto: