2 -
Passo 1
Considere o sistema:
a)
Vamos assumir como a solução do sistema. Portanto iremos substituir esse valor no sistema.
Passo 2
Os valores são as raízes da equação.
Portanto, os autovalores são e .
Passo 3
Quando , a equação fornece,
Cada linha gera a condição:
O autovetor correspondente ao autovalor é:
Passo 4
Encontre o autovetor correspondente ao autovalor .
Substitua na equação ,
Cada linha gera a condição:
O autovetor correspondente ao autovalor é:
Passo 5
b) Como os autovalores obtidos anteriormente são positivos reais, temos que o ponto crítico é um nó instável.
Passo 6
Se a solução começa no ponto inicial na linha através de , então , a solução permanece na linha para todos .
Desde que , como .
Na equação, o termo exponencial positivo é um termo dominante para valores grandes de , de modo que as soluções se aproximam infinitamente assintóticas da linha determinada pela linha .
As únicas linhas são aproximações ao zero e estão exatamente na linha determinada pela linha. Portanto, o ponto crítico é um ponto de sela e instável.
Passo 7
c)
A solução do sistema é:
então e .
E algumas trajetórias terão alguns valores de constantes .
Agora, o esboço das trajetórias é mostrado abaixo:
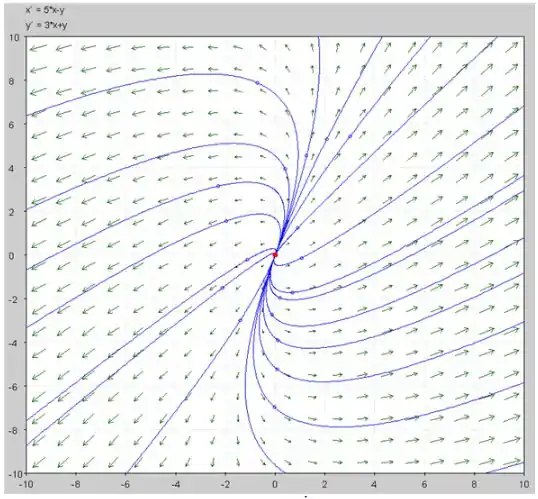
Passo 8
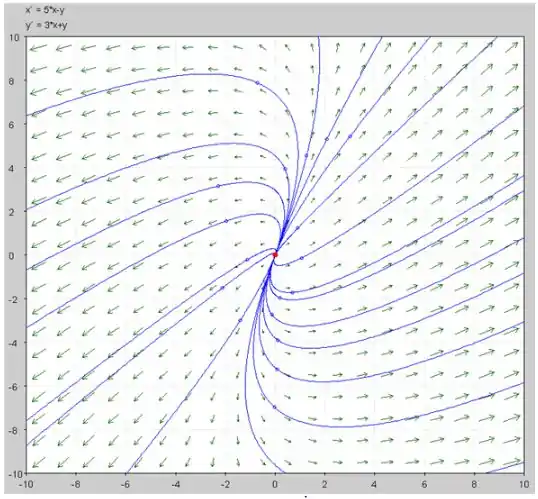
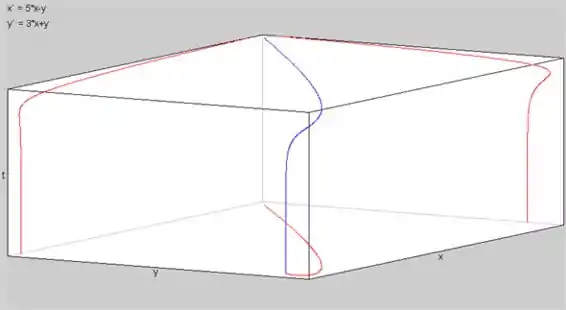
d) O esboço das curvas usando o computador é mostrado abaixo.
Resposta
- Os autovalores são e .
- O ponto crítico é um nó e instável.
O autovetor correspondente ao autovalor é: