Enunciado
Cálculo - Boyce - Equações Diferenciais - Ed: 10º - Capítulo 8.3 - Ex. 14
14. Considere o problema de valor inicial
(a) Desenhe um campo de direções para essa equação.
(b) Estime até onde a solução pode ser estendida para a direita. Seja a extremidadedireita do intervalo de existência dessa solução. O queacontece em que impede a solução de continuar?
(c) Use o método de Runge-Kutta com diversostamanhos de passos para encontrar um valor aproximado de.
(d) Se você continuar os cálculos além de , você pode continuar a gerar valores de . Qual o significado (se algum) desses valores?
(e) Suponha que a condição inicial é modificada para . Repita os itens (b) e (c) para esse problema.
Passo 1
a) Olha só! De antemão, como a criança aqui não é muito bom com desenhos, é importante ir direto ao ponto!
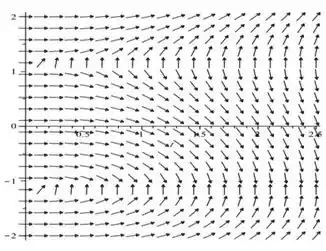
Aqui está nosso campo de direções...
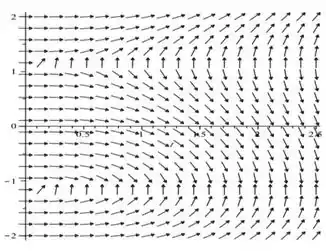
É importante só tomar cuidado com as direções de cada vetor do campo. No nosso caso, eles se reagrupam de forma que olhando direito, parece uma onda de vetores. E cada vetor segue o mesmo padrão, tanto na região quanto na região e .
Passo 2
b) Para resolver esse item, o que temos de fazer é integrar o numerador e denominador e depois simplesmente igualá-los. Afinal, o que essa letra pede é até onde a solução pode ser estendida para a direita.
Vamos começar chamando o numerador de ...
Integrando :
Depois, chamemos o denominador de ...
Integrando :
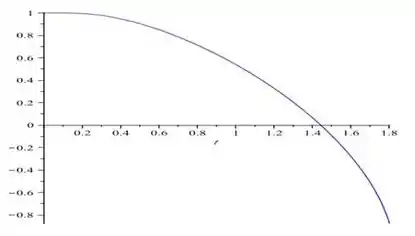
Obtemos então, a seguinte função...
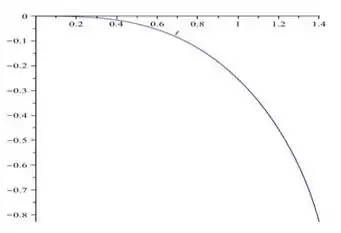
Que plotada em um software, nos mostra o seguinte gráfico:
Passo 3
c) Bora lá agora usar o método de .
Olha só! A nossa já sabemos que é dada por...
E sabemos também das seguintes condições:
Sabendo disso, é uma boa utilizarmos o método de ordem pra resolver esse nosso problema. Assim, iremos obter valores mais aproximados em cada ponto pedido.
A nossa iteração no método de de ordem é dada por...
Agora presta atenção! Como o objetivo é resolver esse problema computacionalmente, o que estamos procurando aqui é fórmulas pra colocarmos em nosso código. De preferência, que estejam em função de e das condições fornecidas pelo enunciado.
Disso isso! Bora pro que interessa! Vamos obter ...
Depois, bora descobrir , que é dado por...
Em seguida, bora partir pra obtenção de , que é igual à...
E finalmente, vamos obter ...
Pronto! Agora vamos pegar esses dados pra usar em nossa resolução computacional.
Passo 4
Para isso, vamos usar a seguinte estrutura abaixo em forma de algoritmo...
Captou a mensagem!?
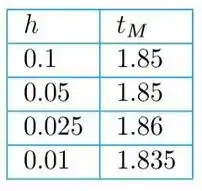
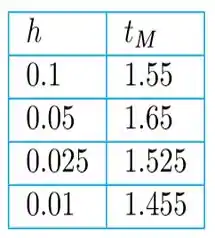
Sendo assim, usando o código já bastante requisitados nas questões anteriores, obtemos os seguintes valores para diferentes tamanhos de passo.
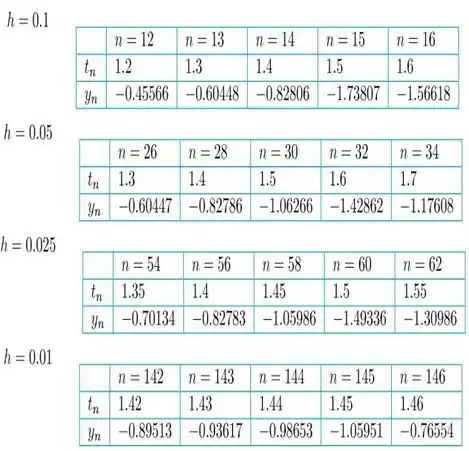
Com base no campo de direção, a solução deve diminuir monotonicamente para o valor limite . Na tabela a seguir, o valor de corresponde ao tempo aproximado no processo de iteração em que os valores calculados começam a aumentar.
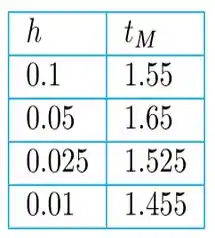
Passo 5
d) Bom! Caso continuemos os cálculos além de , os valores numéricos continuam sendo gerados, embora não sejam associados à curva integral iniciada em Esses valores são aproximados às curvas integrais próximas.
Passo 6
e) Pra finalizar, caso a condição inicial fosse , teríamos que para ...
No caso, a nossa integral ficaria assim...
E não esquecendo da condição inicial...
Obtemos desse modo, a seguinte nova função...
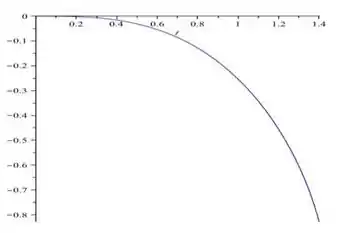
Que ao ser plotado em um software, nos fornece o seguinte gráfico...
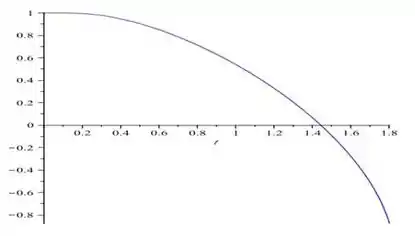
Para a curva integral iniciada em , a inclinação fica infinita perto de . Na tabela a seguir, os valores de correspondem ao tempo aproximado no processo de iteração em que os valores calculados começam a aumentar.
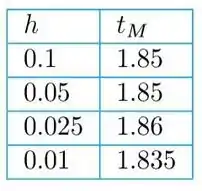
Resposta
a)
b)
c)
d) Os valores numéricos continuam sendo gerados, embora não sejam associados à curva integral iniciada em Esses valores são aproximados às curvas integrais próximas.
e)
