Enunciado
Cálculo - Boyce - Equações Diferenciais - Ed: 10º - Capítulo 9.2 - Ex. 2
2 -
Passo 1
As equações dadas são:
Considere
Primeiro, encontre a solução geral da equação diferencial.
Use o método separável com as seguintes condições iniciais .
Reescreva a equação diferencial (1) como:
Integrando ambos os lados,
Ou
Onde é uma constante arbitrária de integração.
Forme a condição inicial fornecida.
Então,
Portanto, a solução da equação (1) é .
Passo 2
Considere
Então,
Integrando ambos os lados,
Ou
Onde é uma constante arbitrária de integração.
Forme a condição inicial fornecida.
Então,
Portanto, a solução da equação (2) é
Agora com a condição inicial .
Substitua em , para obter .
Passo 3
Agora,
e
Ou,
Integrando ambos os lados,
Ou, .
Use as condições iniciais , para obter:
Portanto, a solução do sistema fornecido é
Passo 4
E a partir do segundo conjunto de condições iniciais , temos:
Portanto, a solução do sistema fornecido é .
Passo 5
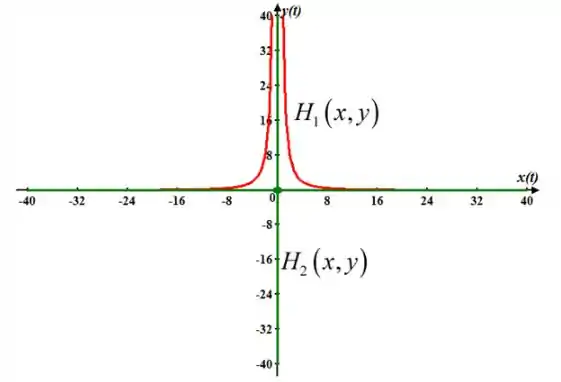
As trajetórias do sistema são dadas por:
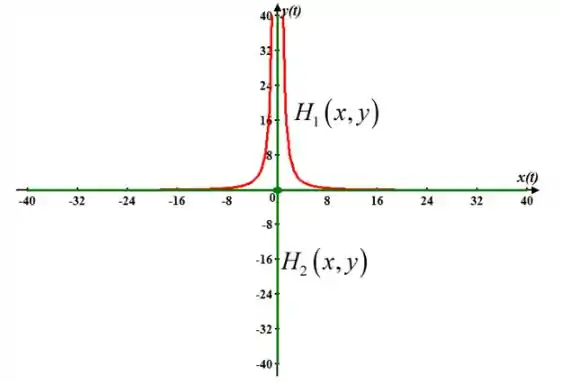
Para determinar a direção do movimento ao longo das trajetórias, veja que, para uma condição inicial positiva, diminuirá enquanto aumentará.
Resposta
