Enunciado
Cálculo - Boyce - Equações Diferenciais - Ed: 10º - Capítulo 9.2 - Ex. 12
12 -
Passo 1
As equações dadas são:
O objetivo é encontrar os pontos críticos para o sistema especificado.
Os pontos críticos são encontrados resolvendo as equações algébricas:
Quando , temos:
Portanto, os pontos críticos são:
Passo 2
b)
O campo de direção é mostrado abaixo:
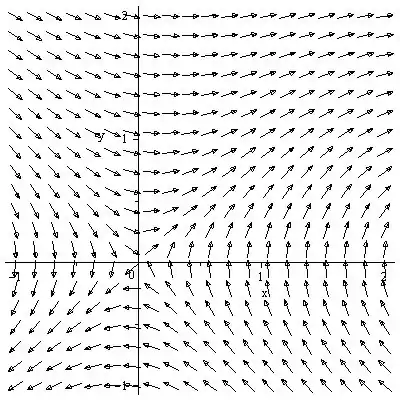
O retrato de fase da equação diferencial é desenhado como abaixo:
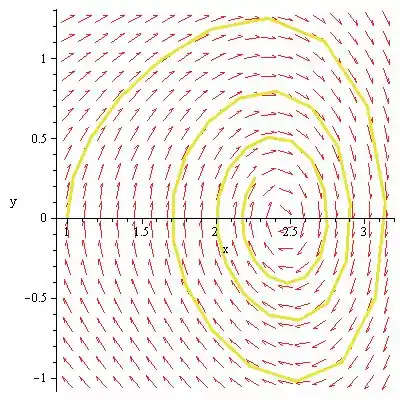
Passo 3
c) Ao comparar determinado sistema com,
Dado,
Então,
O sistema linear sobre um ponto crítico é dado por:
Passo 4
d) Para,
O sistema linear é:
Isso é,
E a equação característica do sistema linear associado é:
Então os autovalores são:
Como os autovalores são reais com sinais opostos, portanto o ponto crítico é um ponto de sela instável.
Passo 5
Para,
O sistema linear é:
Isso é,
E a equação característica do sistema linear associado é:
Então os autovalores são:
Como os autovalores são puramente imaginários, o ponto crítico é um nó assintoticamente estável.
Resposta
- pontos críticos
- O campo de direção é mostrado abaixo:
- O ponto crítico é um nó assintoticamente estável.
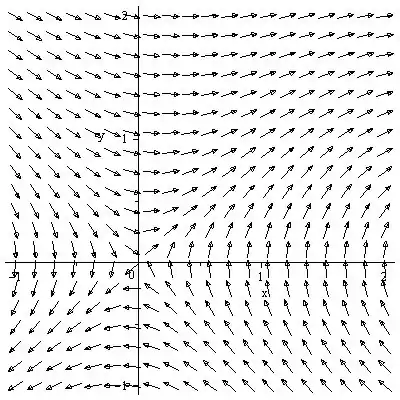
O retrato de fase da equação diferencial é desenhado como abaixo:
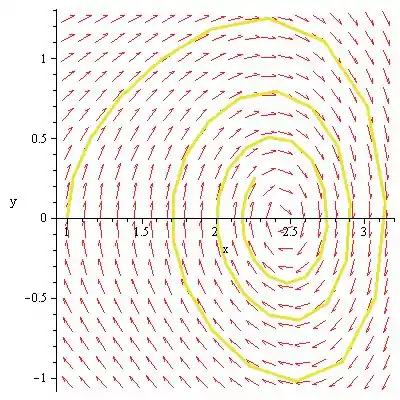
O ponto crítico é um ponto de espiral e assintoticamente estável.
O ponto crítico é uma sela instável.