Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Boyce - Equações Diferenciais - Ed: 10º - Capítulo 9.2 - Ex. 3

3 - (d x)/(d t) = - y , (d y)/(d t) = x ; x (0) = 4 , y (0) = 0 e x (0) = 0 , y (0) = 4 .

Passo 1

As equações dadas são:

(d x)/(d t) = - y e (d y)/(d t) = x

Considere (d y)/(d x) = - (x)/(y) ... . . ( 1 )

Esta equação é separável com:

y d y = - x d x

Integrando ambos os lados,

(y^2)/(2) = - (x^2)/(2) + c_1

Ou,

x^2 + y^2 = c_1

Das condições iniciais fornecidas.

x (0) = 4 , y (0) = 0

Então, c_1 = 16

Portanto, a solução da equação (1) é  x^2 + y^2 = 16 .

Passo 2

Novamente do segundo conjunto de condições

x (0) = 0 , y (0) = 4

Temos c = 16

Portanto, a solução da equação (1) é  x^2 + y^2 = 16 .

Agora, o sistema de equações fornecido também pode ser escrito como:

([[x,'],[y,']]) = ([[0,-,1],[1,0]]) ([[x],[y]])

Vamos tomar como ([[x],[y]]) = X .

Então nós temos  X^' = ([[0,-,1],[1,0]]) X ... . . ( 2 )

Passo 3

Tomemos X = xi e^(r t) .

Então obtemos o sistema algébrico.

([[-,r,-,1],[1,-,r]]) ([[xi_1],[xi_2]]) = ([[0],[0]]) ... ... ( 3 )

Os autovalores são as raízes da equação.

|[[-,r,-,1],[1,-,r]]| = 0

r^2 + 1 = 0

Então os autovalores são  r_1 , r_2 = +- i .

Passo 4

Agora  r = r_1 = i , a equação ( 3 ) fornece:

([[-,i,-,1],[1,-,i]]) ([[xi_1],[xi_2]]) = ([[0],[0]])

Cada linha gera  xi_1 = i xi_2 .

Então o autovetor correspondente é  xi_1 = ([[i],[1]]) .

Passo 5

Da mesma forma, o autovetor correspondente a  r = r_2 = - i é xi_2 = ([[-,i],[1]]) .

Em seguida, duas soluções linearmente independentes são:

x^((1)) (t) = ([[i],[1]]) e^(i t) e x^((2)) (t) = ([[i],[1]]) e^(- i t)

Passo 6

Para encontrar uma solução com valor real, vamos assumir que x^((1)) (t) = ([[i],[1]]) e^(i t) seja

= ([[i],[1]]) ( cos t + i s e n t )

= ([[-,sen t],[cos t]]) + i ([[cos t],[sen t]])

Vamos substituir u (t) = ([[-,sen t],[cos t]]) e v (t) = ([[cos t],[sen t]]) .

Agora  W (u , v) (t) = - 1 , segue-se que  u  e  v  são linearmente independentes e constituem um conjunto fundamental de soluções com valor real.

Então, X = c_1 ([[-,sen t],[cos t]]) + c_2 ([[cos t],[sen t]])

Ou,

([[x],[y]]) = c_1 ([[-,sen t],[cos t]]) + c_2 ([[cos t],[sen t]])

Passo 7

Usando condições iniciais,

x (0) = 4 , y (0) = 0

Nós achamos, c_1 = 0 e c_2 = 4 .

Consequentemente ([[x],[y]]) = ([[4,cos t],[4,sen t]])

Logo, x = 4 cos t e y = 4 sen t .

Passo 8

Agora, usando o segundo conjunto de condições iniciais,

x (0) = 0 , y (0) = 4

Nós achamos  c_1 = 4 e c_2 = 0 .

Então, ([[x],[y]]) = ([[-,4,sen t],[4,cos t]])

Logo, y = 4 cos t e x = - 4 sen t .

Portanto, os dois conjuntos de soluções são:

x = 4 cos t , y = 4 sen t , x^2 + y^2 = 16

x = - 4 sen t , y = 4 cos t , x^2 + y^2 = 16

Passo 9

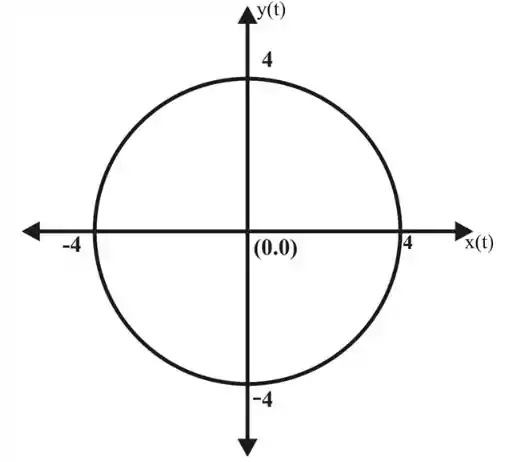
Agora, as trajetórias deste sistema são:

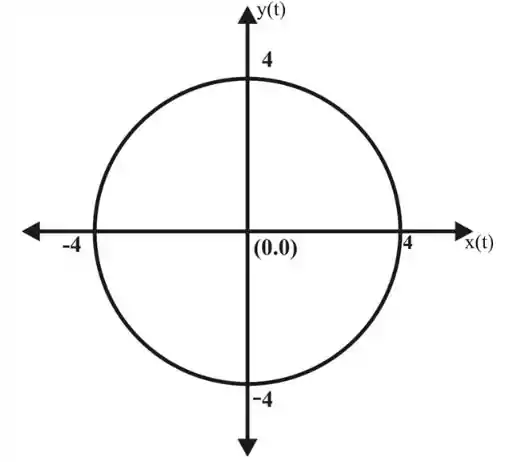
Para determinar a direção do movimento ao longo das trajetórias, vemos que, para condições iniciais positivas, x diminuirá onde y aumentará.

Resposta

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Em cada um dos problemas de 17 a 24 : Encontre uma equação da forma H ( x ,y )=c para as trajetórias.Equações de Duffing: d x d t =y ,d y d t =– x + ( x 3 / 6 )
Em cada um dos problemas de 17 a 24 : Encontre uma equação da forma H ( x ,y )=c para as trajetórias.Pêndulo não amortecido: d x d t =y , d y d t=– s e nx
Em cada um dos problemas de 17 a 24 : Encontre uma equação da forma H ( x ,y )=c para as trajetórias. d x d t =y , d y d t = 2 x + y
Em cada um dos problemas de 17 a 24 : Encontre uma equação da forma H ( x ,y )=c para as trajetórias. d x / d t=– x+y ,d y / d t=– x–y
Em cada um dos problemas de 17 a 24 : Encontre uma equação da forma H ( x ,y )=c para as trajetórias. d x d t=– x + y + x 2, d y d t = y–2 x y