Cabos de pontes suspensas pendurados em parábolas O cabo de ponte suspensa exibido na figura a seguir suporta uma carga uniforme de w libras por pé horizontal. Pode ser demonstrado que, se H é a tensão horizontal do cabo na origem, então a curva do cabo satisfaz a equação:
Mostre que o cabo é pendurado em uma parábola resolvendo essa equação diferencial sujeita à condição inicial de que y = 0 quando x = 0.
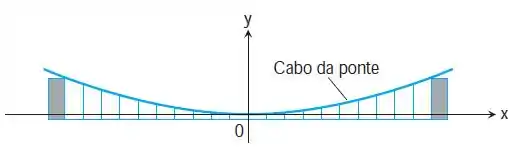
Passo 1
Fala queridos, tudo bom com vocês? Prontos para detonar mais uma questãozinha? Bora! Dentro do parâmetro para a distribuição de carga em função de , temos que:
Agora vamo analisar: quando , temos também que . (no centro da ponte). Dessa forma, aplicando no que acabamos de achar:
Logo,
O que resolve a equação. Dessa forma,
é a equação do cabo.