Enunciado
Cálculo - Cálculo Volume 2 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 10.5 - Ex. 24
Encontre os vértices, os focos e as assíntotas da hipérbole e esboce seu gráfico.
Passo 1
Olá, meu amigo. Nos é dada a equação da hipérbole:
E a gente precisa encontrar os vértices, os focos e a assíntota dela.
A primeira coisa que a gente vai fazer aqui é colocar a equação geral da hipérbole que nos foi dada em formato de característico.
Deveremos chegar no formato:
Com os focos em:
Onde:
Vértices:
E as assíntotas estão em:
Para a gente conseguir colocar nessa forma, iremos precisar completar os quadrados, se você não sabe como fazer isso, irei te ajudar, mas basicamente teremos que colocar os termos de e e um formato de produto notável.
Passo 2
Vamos arrumar com e com dessa expressão dada no enunciado:
O que pode ser escrito da seguinte forma:
A parcela parece muito com:
Assim precisamos inserir nos parênteses onde está
E a parcela parece muito com:
Logo precisamos somar nos parênteses da equação. O que deixa nossa equação da seguinte forma:
Dividindo por os dois lados nós teremos:
Passo 3
Essa equação é uma equação caracterizada por ser uma hipérbole horizontal, com origem em:
E os valores de e serão:
Consequentemente será:
E por ser uma hipérbole horizontal ela terá equações de assíntotas iguais a:
Os focos então estarão em:
E os vértices:
O gráfico estará da seguinte forma:
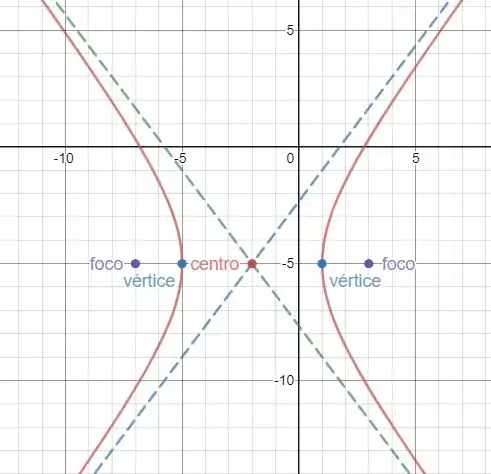
Resposta
Assíntotas:
Focos:
Vértices: