Enunciado
Cálculo - Cálculo Volume 1 - 6ª Edição - James Stewart- Ed: 6º - Capítulo 4.8 - Ex. 4
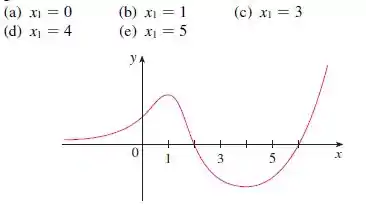
Para cada aproximação inicial, determine graficamente o que acontecerá se for usado o método de Newton para a função cujo gráfico é dado.
Passo 1
Fala aí, tudo bem com você?
Bom, essa questão dá pra gente o seguinte gráfico:
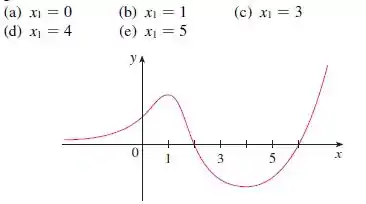
E pede pra gente determinar graficamente o que acontecerá se for usado o método de Newton para essa função.
Para isso, precisamos lembrar que no método de Newton vamos considerar uma reta tangente à curva da função no ponto .
Depois devemos procurar a interseção de como o eixo , que será chamada de e verificar o quão próximo está da interseção da curva com o eixo .
Para encontrar , podemos fazer:
Depois, repetimos o processo, usando como uma segunda aproximação, fazendo:
E podemos repetir o processo quantas vezes for necessário. De modo geral, fazendo
E se ficar cada vez mais próxima da raiz de nossa curva à medida que cresce, fazemos com que a sequência vá para .
Assim:
Show. Então pegaremos essa ideia e aplicaremos graficamente para ver se o método nos levará para a raiz. Vem ver isso acontecendo.
Passo 2
Na letra a, , então neste ponto traçaremos uma reta tangente, onde a reta cruzar com o eixo x será o nosso :
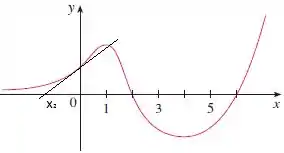
Agora faremos a mesma coisa para o novo ponto e achar
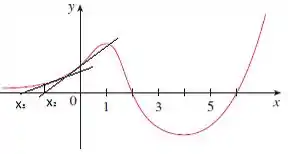
Sendo assim, o x está se afastando cada vez mais da raiz.
Passo 3
Agora, na letra b, , então neste ponto traçaremos uma reta tangente:
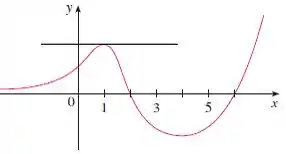
Neste caso a reta tangente é horizontal e não conseguimos achar o ponto e o método falha.
Passo 4
Já vamos para a letra c, onde
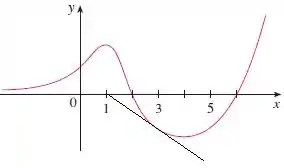
Então o e voltamos ao caso anterior onde o método falha, já que a reta estará se afastando da raiz do nosso gráfico.
Passo 5
Na letra d,
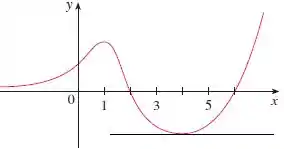
Voltamos ao caso anterior!
Passo 6
Já perceberam a importância da escolha do x não é? Vamos terminar fazendo o mesmo procedimento para a letra e, com
Agora faremos a mesma coisa para o novo ponto e achar
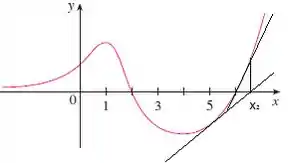
O já se aproxima muito da raiz, e neste caso o método é bem sucedido!