Enunciado
Cálculo - Cálculo Volume 1 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 2.7 - Ex. 12
12.(a) Encontre a inclinação da tangente à parábola nos pontos onde .
(b) Encontre as inclinações das retas tangentes nos pontos cujas coordenadas são (i) (ii) e (iii)
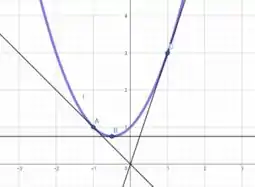
(c) Faça o gráfico da curva e das três tangentes em uma tela comum.
Passo 1
Fala aí, pessoal!
Nesse problema foi dada a equação da parábola
E nosso objetivo é obter a inclinação da reta tangente a nos pontos , , e .
Por fim queremos usar essas informações para esboçar o gráfico de e das retas tangentes.
Parece complicado?
Para obter a inclinação da reta tangente em um ponto qualquer de uma função usamos a equação
Em que , é o coeficiente angular da reta tangente à curva no ponto .
Vamos usar essa fórmula para resolver o item a) e apartir do resultado do item a) substituímos os valores do item b).
Depois de tudo isso analisamos o comportamento da função para esboça-la.
Bora lá!
Passo 2
A equação é dada por
Vamos começar obtendo para substituir no limite
Se , substituímos por ...
Agora fazemos o mesmo para obter (substituímos por em )
Substituindo tudo no cálculo do limite temos:
Organizando esse numerador...
Botando o em evidência para fazermos a redução depois!! Fica dessa forma:
“Cortando” o de cima e de baixo, temos:
Show?
Passo 3
Agora apenas substituiremos o valor de pelos valores do enunciado.
(i)
(ii)
(iii)
Tranquilo até aqui?
Passo 4
Perceba que quanto maior , maior é tambem sua inclinação.
para a inclinação é . Isso significa que nesse ponto a reta tangente é horizontal.
Para a inclinação é , isso significa que a reta tangente é decrescente nesse ponto.
Já em , a inclinação é , logo, a reta tangente é crescente.
Assim podemos dizer que a função tem as seguintes características... quando a função é decrescente e conforme vai chegando em a inclinação tende a ser nula. Por fim, quando a inclinação da reta tangente à função aumenta deliberadamente.
Com isso, esboçando o gráfico da função e as retas tangentes a ela, vamos obter
E aí! o que achou? Responde Aí!
Resposta
()
(i)
(ii)
(iii)
(c)
