Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 1 - 6ª Edição - James Stewart- Ed: 6º - Capítulo 7.1 - Ex. 2

Calcule a integral usando a integração por partes com as escolhasde u e dvindicadas.

∫ θ . cos ⁡ θ . d θ ;               u = θ ,             d v = cos ⁡ θ . d θ

Passo 1

Bom galera, antes de começar vamos lembrar de como funciona a integração por partes:

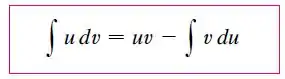
Se já sabemos que é u e quem é dv, basta acharmos du e v:

u = θ → d u = d θ

E

d v = cos ⁡ θ . d θ →     v = s e n   θ

Agora ficou fácil, bora substituir:

∫ θ . cos ⁡ θ . d θ = θ . s e n   θ - ∫ sen ⁡ θ . d θ

Resolvendo a integral que surgiu:

∫ θ . cos ⁡ θ . d θ = θ . s e n   θ - ( - cos ⁡ θ )

∫ θ . cos ⁡ θ . d θ = θ . s e n   θ + cos ⁡ θ + c

Bem tranquilo, não?!

Resposta

∫ θ . cos ⁡ θ . d θ = θ . s e n   θ + cos ⁡ θ + c

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Calcule a integral : ∫ θ cos ⁡ 2 θ + 1 d θ
Calcule a integral : ∫ 1 - v 2 v 2d v
Calcule a integral ∫ x 3 ⋅ e x 2 d x
Calcule a integral ∫ t g - 1 x x 2d x
Calcule a integral ∫ 1 ∞ ln ⁡ y y 3 d y