Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 4.4 - Ex. 75

Cada um dos Exercícios 59-80 fornece a primeira derivada de uma função contínua y = f(x). Determine y" e então use os passos 2-4 do procedimento para construção de gráficos da página 237 para esboçar a forma geral do gráfico de f.

75-

y ' = x + 1 - 2 3

Passo 1

Podemos escrever a equação de y ' da seguinte maneira:

y ' = 1 x + 1 2 3

Logo não temos pontos críticos para essa função uma vez que não tem como y’ ser 0. Somente um crescimento máximo em x = - 1 .

Passo 2

Fazendo a derivada dessa função para acharmos os pontos de inflexão nós temos:

y ' ' = 1 ' x + 1 2 3 - 1 x + 1 2 3 ' x + 1 4 3 = - 2 3 x + 1 - 1 3 x + 1 4 3 = - 2 3 x + 1 5 3

O que também não apresenta y ' ' = 0 , pois essa função não poderá ser 0,(não há valor definido), mas por apresentar também uma mudança muito repentina em x = - 1 por causa do seu denominador, então precisamos observar atentamente o que acontece nesse ponto

Passo 3

Organizando os intervalos:

Teste: -2. 0

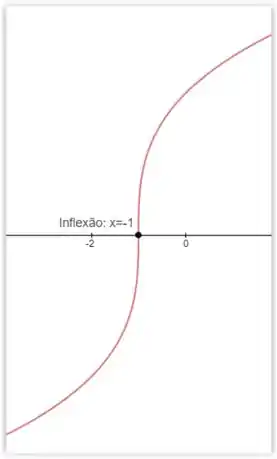
Logo para x = - 1 temos um ponto de inflexão.

Resposta

y ' ' = - 2 3 x + 1 5 3

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Faça um esboço cuidadoso de f e abaixo dele esboce o gráfico de f ’ como foi feito nos Exercícios 4 - 11 . Você pode sugerir uma fórmula para f ‘ ( x ) a partir de seu gráfico? f x = s e n x
Faça um esboço cuidadoso de f e abaixo dele esboce o gráfico de f ’ como foi feito nos Exercícios 4 - 11 . Você pode sugerir uma fórmula para f ‘ ( x ) a partir de seu gráfico? f x = e x
Faça um esboço cuidadoso de f e abaixo dele esboce o gráfico de f ’ como foi feito nos Exercícios 4 - 11 . Você pode sugerir uma fórmula para f ‘ ( x ) a partir de seu gráfico? f x = ln ⁡ x
Encontre a derivada da função dada usando a definição. Diga quais são os domínios da função e da derivada. f x = 1 2 x + 1 3
Seja f x = x 3 .Estime os valores de f ' ( 0 ) ,f ' 1 2 ,f ' ( 1 ) , f ' ( 2 ) e f ' ( 3 ) fazendo uso de uma ferramenta gráfica para fazer um zoom no gráfico de f .Use a simetria para deduzir os valo