Faça um esboço cuidadoso de e abaixo dele esboce o gráfico de como foi feito nos Exercícios . Você pode sugerir uma fórmula para a partir de seu gráfico?
Passo 1
E aí! tudo certinho? 👀

Nesse problema temos que fazer um esboço cuidadoso de e abaixo dele o gráfico de . Além disso temos que sugerir uma fórmula para a partir de seu gráfico.
A função no caso é dada por
Veja só! 😉
Passo 2
Para esboçar o gráfico de vamos primeiro montar uma tabelinha:
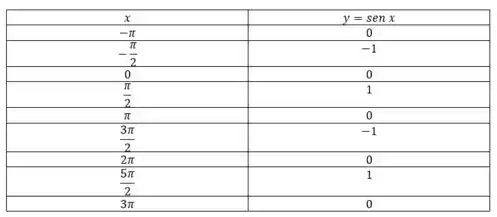
Agora plotando o gráfico:
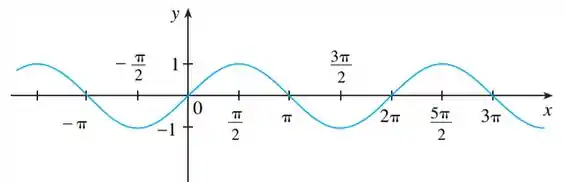
Beleza! Agora que sabemos o formato desse cara, temos que esboçar o gráfico de . Para isso, nós vamos ressaltar alguns pontos importantes no gráfico de : os pontos onde temos tangentes na horizontal (pontos onde a derivada é zero) e pontos onde a tangente tem a inclinação máxima (derivada máxima). Olha só como fica a tangente nesses pontos:
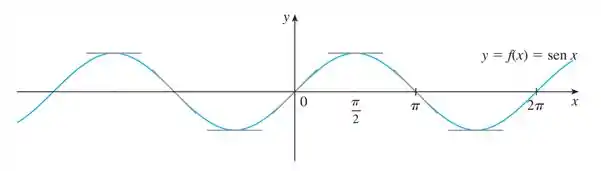
Tranquilo até aqui? 😎
Passo 3
Agora vamos tentar esboçar quem é ! Ah, antes que eu esqueça, vou fazer um lembrete aqui: Quando está crescendo em um intervalo, será positiva. De forma parecida, quando estiver decrescendo, será negativa. Isso é importantíssimo para a gente nesse momento, fechou?
Levando em conta os pontos que destacamos e essa regrinha que acabamos de comentar, olha só como vai ficar o esboço de em comparação com :
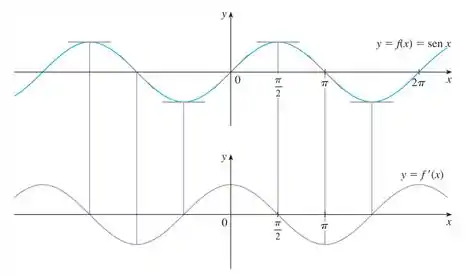
Nosso esboço está pronto! Se analisarmos como ficou , percebemos que seu gráfico será periódico. Olhando também os pontos e , podemos ver que . Deu para notar? Assim temos mais uma pista de quem é !
Analisando o que descobrimos, podemos sugerir que a derivada de é
Dá para sugerir isso, inclusive, se você sabe como é o gráfico função cosseno! Vai perceber que ficou igualzinho ao da nossa derivada ;)
E aí! o que achou? Responde Aí! 😁
Resposta
O esboço de vai ficar dessa forma:
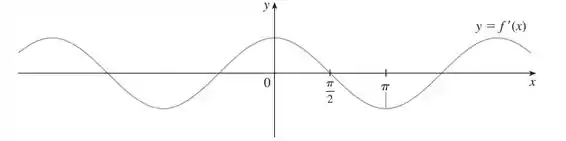
E a expressão que podemos sugerir para essa derivada é .