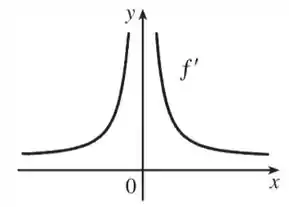
Trace ou copie o gráfico da função dada. (Suponha eixos com a mesma escala.) Use então o método do Exemplo para esboçar o gráfico de .
Passo 1
Preparados para mais um exercício sobre gráficos de derivadas? Sim? Então bora lá!
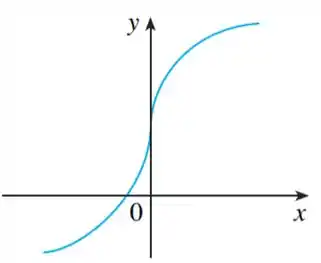
O problema nos da a curva da função :
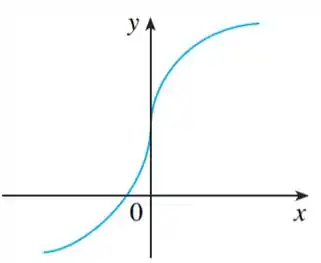
E pede pra a gente traçar a curva de usando como base o exemplo 1 do livro. Nesse exemplo tínhamos isso daqui:
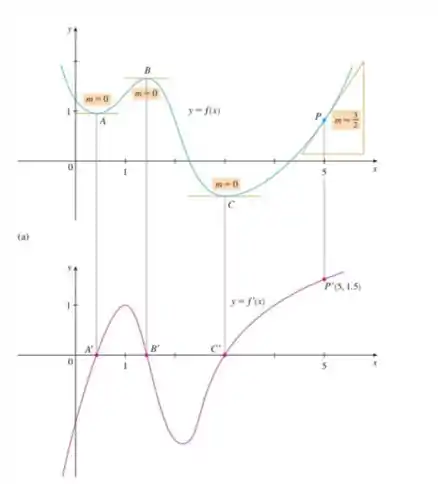
Ou seja, para esboçar o gráfico da derivada, temos que prestar atenção em alguns pontos do gráfico original. Nos intervalos onde a função decresce, a derivada será negativa. Nos casos em que cresce, será positiva, não se esqueçam!
Vale ressaltar também que, quanto mais rápido ta aumentando ou diminuindo os valores na função, mais longe o eixo estarão os pontos correspondentes no gráfico da derivada, beleza? Isso vai ajudar a dar o formato do desenho.
Além disso, temos que procurar os pontos onde temos uma tangente na horizontal – como a derivada é a inclinação da reta tangente, nesses pontos, a será zero.
Ah, uma coisa importantíssima aqui: Teremos um ponto onde a derivada não vai existir! Isso vai acontecer porque encontraremos uma tangente na vertical quando analisarmos o gráfico de , beleza? S-E-M-P-R-E que isso rolar com algum ponto em alguma função, não vamos ter a derivada nesse ponto. Isso é regra, fechou?
Bora lá?!
Passo 2
Agora, vamos começar a nossa análise do gráfico! P
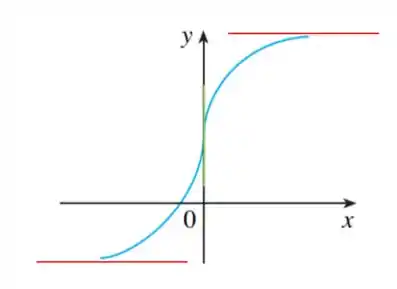
Podemos observar que temos duas assíntotas horizontais, uma no eixo negativo e outa no postivo.
Isso significa que a inclinação tende a zero quando no lado esquerdo do gráfico e no lado direito!
Além disso temos uma reta tangente vertical em , qual seria o valor dela?!
Lá da trigonometria a gente tem que:
E em que ângulo a gente tem uma reta vertical?! Em , certo?!
E qual é a tangente de ? Ela vai ser a inclinação da reta nesse ponto! Vamos calcular então:
Putz, indeterminação! Então esse vai ser um ponto de descontinuidade na curva da derivada!
Tem mais, podemos dizer que:
Já que temos uma divisão por zero. Isso significa que vamos ter uma assíntota vertical quando nos aproximamos do ponto onde a reta tangente é horizontal!
Passo 3
Depois de todas essas considerações, podemos esboçar o gráfico:
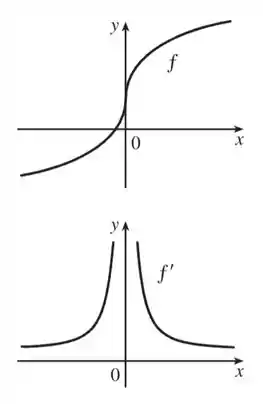
Temos a assíntota vertical em e as assíntas verticais quando !
Resposta
O esboço de será o seguinte: