Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 2.8 - Ex. 15
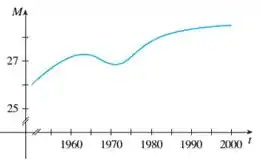
O gráfico mostra como a idade média dos homens japoneses quando se casam pela primeira vez variou na última metade do século XX. Esboce o gráfico da função derivada . Em quais os anos a derivada foi negativa?
Passo 1
Fala aí! tudo certinho? 😬
Nesse problema foi dado um gráfico de uma função e nosso objetivo é determinar os valores onde a derivada dessa função é negativa.
Parece complicado? 😉
Para resolver esse exercício aqui, precisamos relembrar de algumas regras sobre o esboço do gráfico de derivadas a partir do gráfico original, beleza?
- Em primeiro lugar, toda vez que o gráfico estiver com seus valores crescendo, teremos uma derivada positiva. Acontece de forma similar quando os valores do gráfico estão diminuindo – teremos a derivada negaiva.
- Em segundo lugar, toda vez que tivermos um ponto de máximo ou de mínimo, a derivada lá vai ser zero. Isso acontece porque, se traçarmos a reta tangente nesse ponto específico, termos uma reta na horizontal, ou seja, sem inclinação, dessa forma a sua derivada nesse ponto é zero!
Veja só! 😁
Passo 2
Vamos desenhar agora um diagrama mostrando onde o gráfico ta crescendo, decrescendo e onde temos retas tangentes na horizontal. Saca só como vai ficar:
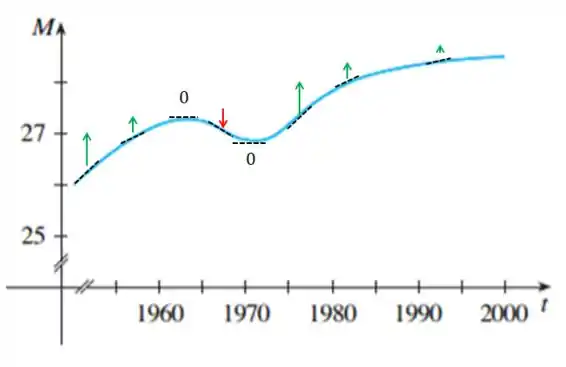
Percebe que eu não coloquei só onde a função cresce ou decresce, mas o quanto ela cresce ou decresce. Afinal, quanto maior o crescimento, maior será a derivada naquele ponto.
Com as informações que conseguimos, podemos esboçar o nosso gráfico de ! Basta só que sigamos as regras ditas no passo um e façamos com bastante calma. Olha só como vai ficar o esboço:
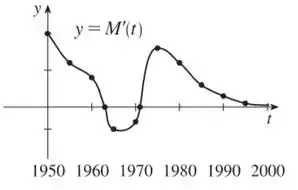
Perceba que no gráfico de , quando se aproxima de , se você desenhar uma reta tangente, ela vai ficando quaaase na horizontal. No nosso gráfico de , a medida que nos aproximamos de , nosso gráfico vai ficando quaaase no zero, tranquilo?
Passo 3
Com o esboço do gráfico , dá para ver também que tem derivada negativa mais ou menos entre os anos de e .
Respondido isso, terminamos esse exercício! Uhul!
E aí! o que achou? Responde Aí! 😊
Resposta
O esboço do gráfico de será:
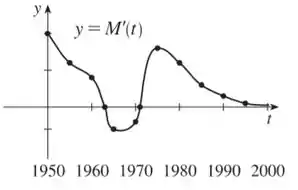
Com a derivada sendo negativa entre os anos de e .