Faça um esboço cuidadoso de e abaixo dele esboce o gráfico de como foi feito nos Exercícios . Você pode sugerir uma fórmula para a partir de seu gráfico?
Passo 1
A primeira coisa que temos que fazer aqui é desenhar o gráfico da nossa função exponencial . Ele é desse jeito aqui:
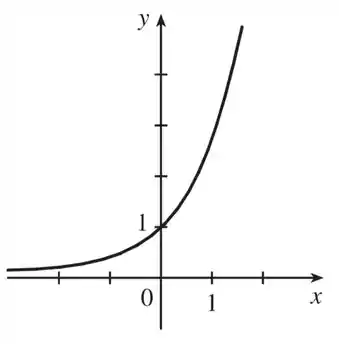
Esse gráfico é um daqueles que tem que ta na cabeça como é o gráfico o tempo todo, fechou? Vai ajudar que só isso nas próximas lições de cálculo, então fica a dica!
Passo 2
Nosso próximo passo vai ser desenhar algumas retas tangentes no gráfico da exponencial para ter uma ideia do que esperar do gráfico de sua derivada. A próxima imagem mostra algumas dessas retas, saca só:
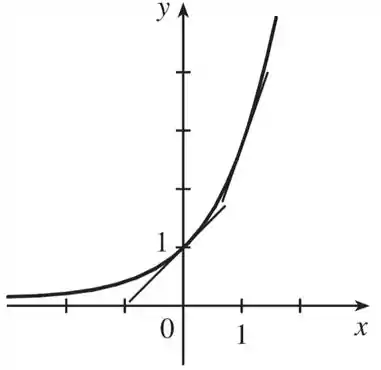
Já podemos tirar algumas conclusões de como vai se comportar – a primeira é que, pelo visto, as retas tangentes à sempre vão ser crescentes, então a função vai ser sempre positiva!
Outra conclusão é que, a medida que caminhamos no gráfico da exponencial para a direita no eixo , essas retas tangentes vão ficando mais e mais inclinadas, ou seja, o valor da derivada aumenta cada vez mais!
Passo 3
Outra coisa que dá para fazer é estimar quem é a derivada no ponto , que vai ser a inclinação da reta tangente no mesmo ponto. Para estimar a inclinação da reta, primeiro a gente vai fazer um triângulo na nossa figura, dá uma olhada:
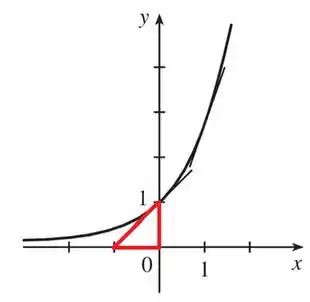
Podemos estimar o valor da inclinação por essa fórmula aqui:
Onde vai coincidir com a altura do nosso triângulo e com a largura. Bom, parece que a largura dele é de aproximadamente unidade e a altura é de , logo:
Ou seja: a nossa derivada vai valer quando . Beleza! Sabemos então que o gráfico de vai ter o ponto
Passo 4
Com o que descobrimos dá para ter uma ideia já de como vai ficar o gráfico de . Recapiulando o que descobrimos, sabemos que a nossa derivada só tem valores positivos para qualquer intervalo de e, conforme cresce, os valores da derivada vão subindo mais e mais. Além disso, estimamos que o nosso gráfico passa pelo ponto . Juntando tudo isso, nosso esboço vai ficar assim:
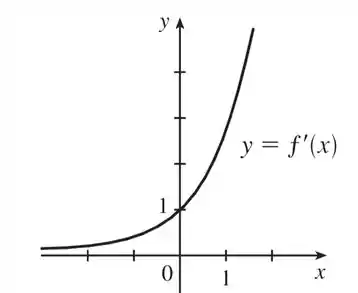
Olha aí nosso que coisa linda! Mas pera lá: ele ta igualzinho ao nosso ! Se eles tão iguais, de cara podemos sugerir que o gráfico de , concorda? E é isso mesmo: a derivada da exponencial é ninguém mais e ninguém menos que a própria exponencial! Bem louco né? XD
Resposta
O esboço de vai ficar dessa forma:
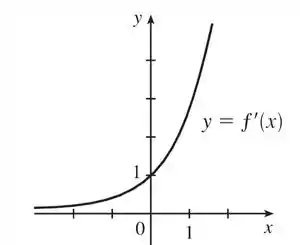
E a expressão que podemos sugerir para essa derivada é .