Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 6.2 - Ex. 44

Ache o volume do sólido gerado pela rotação da região fora da curva y = x 2 e entre as retas y = 2 x - 1 e y = x + 2 em torno do eixo y .

Passo 1

A questão pede o volume do sólido gerado pela rotação em torno do eixo y da região externa à parábola y = x 2 e entre as retas y = 2 x - 1 e y = x + 2 .

A região que será rotacionada em torno do eixo y é a região limitada pelos pontos indicados.

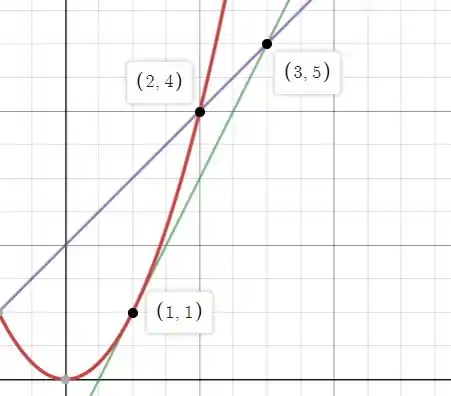
Para resolve esse problema vamos usar o método das cascas cilíndricas (invólucro cilíndrico):

V = ∫ a b 2 π x f x   d x

Mas neste caso, f será a diferença entre as funções (“altura”) e ainda teremos que quebrar a integral em duas: uma que f x = x 2 - 2 x - 1 = x 2 - 2 x + 1 e outra em que f x = x + 2 - 2 x - 1 = - x + 3 . Assim,

V = 2 π ∫ 1 2 x   x 2 - 2 x + 1   d x + 2 π ∫ 2 3 x   3 - x   d x

Ou ainda

V = 2 π   ∫ 1 2 x 3 - 2 x 2 + x   d x + ∫ 2 3 3 x - x 2   d x

Passo 2

Assim, fazendo as integrais:

V = 2 π   x 4 4 - 2 x 3 3 + x 2 2 1 2 + 3 x 2 2 - x 3 3 2 3

Portanto,

V = 2 π   4 - 16 3 + 2 - 1 4 + 2 3 - 1 2 + 27 2 - 9 - 6 + 8 3

Assim,

V = 2 π   - 9 - 6 3 + 26 2 - 1 4 = 2 π   - 9 - 2 + 13 - 1 4

Logo,

V = 2 π   2 - 1 4 = 2 π ⋅ 7 4 = 7 π 2

Resposta

7 π 2

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

43 - Deduza a fórmula do volume de um cone circular reto de altura h e raio r usando um sólido de revolução adequado.
42 – Um bolo em forma de anel é formado pela rotação em torno do eixo y da região limitada pleo gráfico de y = s e n ( x 2 - 1 ) e pelo eixo x ao longo do intervalo 1 ≤ x ≤1 + π . Determine o volume d
48- Determine o volume do sólido da região limitada pelos gráficos de y = e x 2 , y = 1 e x = ln ⁡ 3 obtido com a rotação do eixo x .
47- Determine o volume do sólido da região limitada pelos gráficos de y = e - x 2 , y = 0 , x = 0 e x = 1 obtido com a rotação em torno do eixo y .
46- A região entre a curva y = sec - 1 ⁡ x e o eixo x de x = 1 até x = 2 (mostrada aqui) é girada em torno do eixo y para gerar um sólido. Determine o volume do sólido.