O gráfico da primeira derivada de uma função está mostrado.
(a) Em que intervalos está crescendo? Explique.
(b) Em que valores de a função tem um mínimo ou máximo local? Explique.
(c) Em que intervalos é côncava para cima ou para baixo? Explique.
(d) Quais são as coordenadas dos pontos de inflexão de ? Por quê?
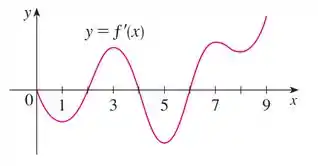
Passo 1
Olá, meu amigo. Yuri aqui e estarei te ajudando a resolver essa atividade.
Nessa questão, temos o gráfico da derivada de uma função.
A derivada é assim ó:
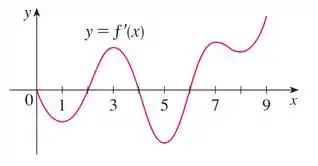
Na letra a), a partir do gráfico temos que encontrar os intervalos em que está crescendo.
Isso vai ocorrer nos intervalos em que a derivada for positiva, o que indica uma inclinação positiva na função e portanto que a função cresce nesses intervalos.
Na letra b) queremos os pontos de máximo ou mínimo local.
Para isso, basta olharmos para quando a derivada é zero.
Esse é um ponto crítico.Ele será um ponto de máximo, caso a derivada antes dele seja positiva e depois negativa (pois assim a função crescia, chegou no máximo e depois passou a decrescer) e ele será um ponto de mínimo, caso a derivada antes dele seja negativa e depois positiva (pois assim a função diminuía, chegou no mínimo e depois passou a crescer).
Já na letra c), queremos saber sobre os intervalos de concavidade para cima e para baixo.
Sabemos que a função é côncava para cima quando
E é côncava para baixo quando
Para isso, vamos ter que olhar para a derivada da derivada (a segunda derivada).
Aqui nós só temos o gráfico da derivada, portanto, não tem como derivar uma expressão numérica para chegar na segunda derivada.
Mas olhando para o gráfico, sabemos como é a segunda derivada.
Quando o gráfico da derivada cresce, isso indica que a segunda derivada é positiva e, portanto, a concavidade é para cima.
E quando o gráfico da derivada decresce, isso indica que a segunda derivada é negativa e, portanto, a concavidade é para baixo.
Por fim, na letra d), temos que indicar os pontos de inflexão.
Eles ocorrem quando
Nesse caso, vamos olhar pro gráfico da derivada e ver quando sua inclinação é zero (a função nem cresce nem decresce), isso indica que a segunda derivada é nula.
Bora lá
Passo 2
Letra a)
está crescendo nos intervalos onde , que são: e .
Passo 3
Letra b)
tem um máximo onde ela passa de crescimento para decrescimento, que pelo gráfico, é onde muda de positivo para negativo, em .
Seguindo o mesmo raciocínio, tem um ponto de mínimo onde ela passa de decrescimento para crescimento, e onde muda de negativo para positivo, em e .
Passo 4
Letra c)
Quando está crescendo, é positivo, e consequentemente, é côncava para cima.
Isso acontece em e em
Da mesma forma, é côncava para baixo quando está decrescendo, que é em e em .
Passo 5
Letra d)
tem pontos de inflexão em e , pois é onde a derivada tem vértices, onde a sua derivada é nula, e portanto a segunda derivada da função é nula.
Resposta
- e .
- Mínimo local: e .
- Para cima: e em
- e .
Máximo local: .
Para baixo: e em .