Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 4.3 - Ex. 5
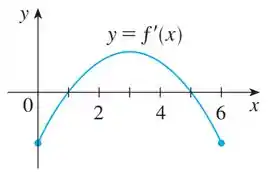
O gráfico da derivada de uma função está mostrado.
(a) Em quais intervalos é crescente ou decrescente?
(b) Em que valores de a função tem um mínimo ou máximo local?
Passo 1
Olá, meu amigo. Yuri aqui e estarei te ajudando a resolver essa atividade. Aqui deveremos analisar o comportamento da função a partir do gráfico de sua derivada.
Passo 2
Vamos dar uma olhada na letra a)
Perceba que quando uma função é crescente, a reta tangente ao seu gráfico terá uma inclinação positiva, e essa inclinação é dada justamente pelo valor na derivada da função naquele ponto.
Como o enunciado nos deu o gráfico da derivada da função , para determinar os intervalos onde a função é crescente, basta olharmos em quais intervalos o gráfico da derivada possui valores positivos.
é crescente se
E perceba que isso acontece no intervalo .
Pensando de maneira parecida, a função será decrescente quando a sua derivada possuir valores negativos
é decrescente se
E isso acontece em e em .
Passo 3
Agora vamos falar da letra b)
Como temos em , e muda de positivo para negativo, muda do crescimento para o decrescimento, então um ponto de máximo.
Como temos em , e muda de negativo para positivo, muda de decrescimento para crescimento, isso quer dizer que esse é um ponto de mínimo.
Resposta
- é crescente em e decrescente em e em .
- Há máximo em e um mínimo em .