Enunciado
Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 5.7 - Ex. 1d
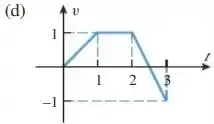
Em cada parte, é dada a curva velocidade versus tempo de uma partícula que se move ao longo de uma reta. Use a curva para encontrar o deslocamento e a distância percorrida pela partícula no intervalo de tempo .
Passo 1
Faaala aí, pessoal! Prontos pra mais um exercício com o Responde Aí?
Bom, para esse exercício em questão, precisamos aplicar a integral para fazer o cálculo das funções de movimento, como deslocamento, velocidade e aceleração. Para o caso em questão, o que é pedido é apenas o deslocamento de uma partícula e a distância que ela percorreu em um determinado intervalo de tempo.
Então, lembrando da relação entre velocidade e posição:
Usando a integral, para um intervalo de tempo , o deslocamento da partícula será dado por:
E a distância total percorrida pela partícula será dada por:
Passo 2
Então, como a curva dada é uma curva da velocidade em relação ao tempo, podemos descobrir o valor ou a função que define a velocidade.
Logo, para o exercício , a função velocidade será dada por uma função de primeiro grau para cada inclinação da reta:
E
E
Assim, o deslocamento pode ser escrito pela integral:
Que, calculada, resulta em:
E, substituindo o intervalo de integração (que é o intervalo de tempo que a partícula percorreu), teremos:
Ou seja:
Passo 3
Fazendo da mesma forma, vamos calcular a distância percorrida pela partícula através da integral citada. Então, para cada intervalo, a velocidade assumirá valores positivos e negativos, tal que:
Para , a velocidade é positiva e, logo:
Como em , a velocidade é positiva, o seu módulo assumirá o valor oposto:
No entanto, para o intervalo , o módulo da velocidade será dado por dois valores diferentes, visto que a velocidade muda de sinal no meio desse intervalo. Então:
Para
E para
Dessa forma:
Que resulta em:
E, substituindo o intervalo de integração, teremos:
Portanto: