Enunciado
Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 5.7 - Ex. 3b
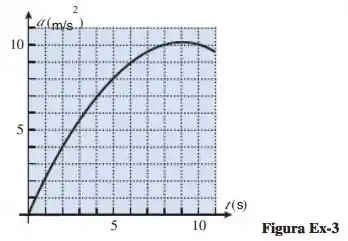
A figura a seguir mostra a curva a aceleração versus tempo de uma partícula que se move ao longo de um eixo. Se a velocidade inicial da partícula for de , estime
a velocidade no instante ;
a velocidade no instante .
Passo 1
Faaala aí, pessoal! Prontos pra mais um exercício com o Responde Aí?
Bom, para esse exercício em questão, precisamos aplicar a integral para fazer o cálculo das funções de movimento, como deslocamento, velocidade e aceleração. Para o caso em questão, o que é pedido é a velocidade de uma partícula em determinados instantes de tempo.
Então, lembrando da relação entre velocidade e aceleração:
Usando a integral, para um intervalo de tempo , a velocidade da partícula será dada por:
No entanto, precisamos incluir outra informação nessa equação. Como a partícula não parte do repouso, precisamos acrescentar a velocidade inicial que foi dada no enunciado:
Ou seja:
Passo 2
Porém, como a função que define a aceleração não é dada, não conseguimos calcular a integral apenas pela substituição da função. Mas não tema! Conseguimos encontrar o resultado através de outro caminho.
Lembrando que a integral representa a área sob uma curva dada, podemos aplicar esse princípio para o cálculo da nossa integral da aceleração, somando as pequenas áreas em cada coluna de quadrados do gráfico aceleração versus tempo.
Dessa forma, supondo que cada quadrado tenha dimensões de , vamos somar a área embaixo da curva da aceleração em cada intervalo de .
Passo 3
Logo, fazendo um esboço, aproximando a curva à uma linha reta, e separando cada coluna de quadrados, temos que analisar qual é a área abaixo da curva (que está representada no esboço pela linha vermelha):
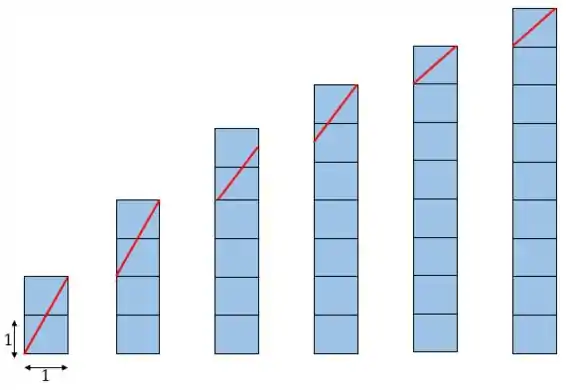
Logo, para a primeira coluna podemos fazer uma área de triângulo:
E para as outras colunas podemos aplicar a fórmula da área de um trapézio:
Assim, o cálculo da nossa velocidade se dará por:
E, como os valores das “mini áreas” são aproximados, teremos:
A diferença do valor real se dá por causa da aproximação feita através de uma reta ao invés da própria curva.