Exercícios de Propriedades das Integrais - Lista de Exercícios Resolvida

Use as propriedades das integrais para verificar a desigualdade sem calcular as integrais.

Se , e , determine:

Escreva como uma integral única na forma :

Dada a seguinte integral dupla

1. Desenhe a região de integração.

Calcular a área delimitada por e .

A intersecção será correspondente a e a área

A intersecção será correspondente a e a área

A intersecção será correspondente a e a área

A intersecção será correspondente a e área

Sejam e A área da região limitada pelos gráficos de e e pelas retas e é igual a:

Calcular a área delimitada por e .

A intersecção será correspondente a e a área

A intersecção será correspondente a e a área

A intersecção será correspondente a e a área

A intersecção será correspondente a e área

A fórmula é válida sob que condições?

Escolha uma opção:

Para todo

Somente para

Para todo

Para todo

Somente para

Avalie as seguintes integrais:

Determine se converge ou diverge, se convergir, determine seu valor.

Mostre que a integral converge.

Determine se converge ou diverge.

Determine se converge ou diverge.

Mostre que a integral converge.

Seja e calcule

Calcule as integrais

Calcule as integrais

Resolva as integrais seguintes:

a)

Resolva as integrais seguintes:

a) Inspirada na galinha dos ovos integrais (SQ1733)

1. A integral definida é representada pelo limite:

1.5 Dada a integral , considere as seguintes afirmações:

Utilize a tabela do exercício anterior (ver tabela abaixo) para calcular as integrais indefinidas abaixo:

Utilize a tabela do exercício anterior (ver tabela abaixo) para calcular as integrais indefinidas abaixo:

Utilize a tabela do exercício anterior (ver tabela abaixo) para calcular as integrais indefinidas abaixo:

Utilize a tabela do exercício anterior (ver tabela abaixo) para calcular as integrais indefinidas abaixo:

Utilize a tabela do exercício anterior (ver tabela abaixo) para calcular as integrais indefinidas abaixo:

Utilize a tabela do exercício anterior (ver tabela abaixo) para calcular as integrais indefinidas abaixo:

Utilize a tabela do exercício anterior (ver tabela abaixo) para calcular as integrais indefinidas abaixo:

Uma partícula se move ao longo do eixo x com uma função velocidade . Qual a distância percorrida pela partícula entre e

Utilize a tabela do exercício anterior (ver tabela abaixo) para calcular as integrais indefinidas abaixo:

Seja o campo vetorial dado por :

O campo vetorial é conservativo? Caso seja positivo, encontre a função potencial tal que ;

Calcule o trabalho realizado pelo campo de força acima, ao mover um objeto ao longo da curva dada pela função , .

Encontre a integral indefinida.

c)

Encontre a integral indefinida.

f)

Encontre a integral indefinida.

a)

Calcule as integrais:

a)

Sejam e funções contínuas com:

Calcule as seguintes integrais:

Sejam e funções contínuas com:

Calcule as seguintes integrais:

Sejam e funções contínuas com:

Calcule as seguintes integrais:

Sejam e funções contínuas com:

Calcule as seguintes integrais:

Calcule:

Calcule:

Resolva a integral

Resolva a integral

Resolva a integral

Resolva a integral

Resolva a integral

Resolva a integral

Calcule:

Resolva a integral

Resolva a integral

Resolva a integral

Resolva a integral

Resolva a integral

Seja , definida abaixo:

1. Determine se é inversível em seu domínio.
2. Determine quantas raízes possui.

Sejam e funções contínuas com:

Calcule as seguintes integrais:

Resolva a integral

Resolva a integral

Sejam e funções contínuas com:

Calcule as seguintes integrais:

Sejam e funções contínuas com:

Calcule as seguintes integrais:

Sejam e funções contínuas com:

Calcule as seguintes integrais:

Resolva a integral

Calcule:

Calcule:

Resolva a integral

Resolva a integral

Resolva a integral

Resolva a integral

Resolva a integral

Resolva a integral

Resolva a integral

Resolva a integral

Sejam e funções contínuas com:

Calcule as seguintes integrais:

Sejam e funções contínuas com:

Calcule as seguintes integrais:

Sejam e funções contínuas com:

Calcule as seguintes integrais:

Calcule:

Resolva a integral

Resolva a integral

4 – Calcule a seguinte integral definida:

Utilize a tabela do exercício anterior (ver tabela abaixo) para calcular as integrais indefinidas abaixo:

Utilize a tabela do exercício anterior (ver tabela abaixo) para calcular as integrais indefinidas abaixo:

4) Calcule cada uma das integrais abaixo.

(f)

Encontre a integral indefinida.

e)

Dado , considere a função , definida para .

1. Verifique a derivada de f coincide com a derivada de , no intervalo
2. Usando o item acima e o exercício anterior, conclua que , para alfuma . Em seguida, faça nestaa igualdade para calcular o valor da constante C
3. Conclua que

3. Extras

a) Para a função dada abaixo, esboce seu gráfico e em seguida calcule

Encontre a integral indefinida.

b)

Encontre a integral indefinida.

d)

Seja

1. Determine .

Seja uma função contínua e defina:

1. Para e pequeno, use as propriedades da integral e o Teorema da

Média para verificar que

para algum .

2. Usando o item anterior e a continuidade de f, mostre que
3. Repita o argumento acima para , e conclua que a função e derivável e
4. Supondo agora que é uma primitiva qualquer de f, mostre que

Sejam e A área da região limitada pelos gráficos de e e pelas retas e é igual a:

Suponha que, no instante , a posição em relação à origem de uma partícula que se desloca ao longo de uma reta seja dada por em que é a função velocidade, cujo gráfico está ilustrado abaixo. Considere ainda que seja dado em segundos, que seja dada em metros e que, para , o gráfico de seja um segmento de reta. A partir do gráfico da função velocidade, julgue os itens a seguir.

1. A partícula está se afastando da origem entre os instantes .
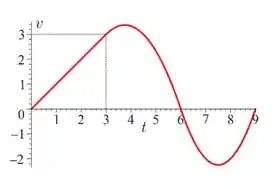
2. A partícula percorre menos de metros nos primeiros segundos.
3. No instante a partícula está na origem.
4. No instante a posição da partícula é positiva.
5. O espaço total percorrido pela partícula igual a

9.9 Verifique se é convergente ou divergente. Caso seja convergente, você consegue estimar o valor desta integral?

9.5 Seja definida para . Mostre que é crescente.

9.11. Verifique se é convergente ou divergente.

10.5 Decida se cada afirmação é verdadeira ou falsa. Justifique as verdadeiras e corrija adequadamente as falsas.

b) Se , então .

10.5 Decida se cada afirmação é verdadeira ou falsa. Justifique as verdadeiras e corrija adequadamente as falsas.

c) se , então .

10.7 Decida se a integral

É convergente ou divergente. Caso seja convergente, calcule seu valor.